Encontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Passo 1
Fala galera, tudo beleza?
Nessa questão estamos trabalhando com as queridíssimas funções de duas variáveis.
Recebemos a função:
E, precisamos calcular o seu domínio e a sua imagem.
Vocês lembram o que é o domínio e o que é a imagem?
É legal pensar numa analogia da função como sendo uma liquidificador. O domínio é o conjunto de todos os ingredientes que você pode colocar dentro do liquidificador (não dá pra colocar tudo, algumas coisas quebraria o aparelho, certo?).
Já a imagem é o que o liquidificador produz após bater todos aqueles ingredientes, sacaram?
Então, nossa ideia é primeiro verificar as possíveis restrições na nossa lei de função para encontrar o domínio de .
Em seguida, vemos os possíveis valores que esse domínio pode nos dar em .
Vem com a gente que vai ficar bem claro 😊
Passo 2
Bom, vamos começar analisando a nossa função :
A expressão dentro do arcoseno representa justamente o valor do seno de . Como representa o valor de um seno, precisa obrigatoriamente estar no intervalo:
Assim:
E:
Assim, o domínio de pode ser escrito como:
Essa região, representada graficamente, fica:
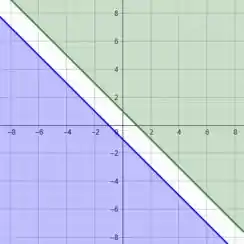
Onde o nosso domínio é justamente a parte branca entre as duas regiões sombreadas.
Passo 3
Vamos agora pensar na imagem da função. Temos:
Existem diversos ângulos que resultam no mesmo valor de seno, ou seja, existem diversos cujo seno resultam em . Para eliminar esse problema as funções seno sempre consideram que o contradomínio está entre:
Como abrange todos os valores entre e temos que a imagem de compreende:
Sacaram?
É isso gente, até a próxima 😊