Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 104123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFJF. Cálculo 3. Lista de Estudos. Lista da AV1 – 2022.2. Questão 3.

3. Calcule a área da região R delimitada pelas circunferências x 2 + y 2 = 2 3 x e x 2 + y 2 = 6 x .

Passo 1

Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão foi dada uma região R delimitada pelas equações de circunferências x 2 + y 2 = 2 3 x e x 2 + y 2 = 6 x .

Nosso objetivo, é calcular a área dessa região R .

O que temos que fazer para obter esse resultado? 🤔

Quando queremos calcular a área abaixo de uma superfície, estamos calculando a integral dessa superfície. No enunciado, foi dito que a região R é delimitada por circunferências, então para calcular essa integral vamos converter as coordenadas retangulares x y para coordenadas polares r θ .

Mas antes, vamos dar uma olhada na nossa região de integração!

Bora lá! 😁

Passo 2

Uma das circunferências que delimitam nossa região é dada por

x 2 + y 2 = 2 3 x

Essa equação do jeito que está, não é tão fácil visualizar como é o gráfico dessa circunferência.

Então vamos organizá-la um pouquinho

x 2 - 2 3 x + y 2 = 0

Podemos reescrever x 2 - 2 3 x como a 2 - 2 a b + b 2 = a - b 2 com a = x e b = 3 , mas perceba que falta nosso termo b 2 , não é? Então para não interferir na equação, vamos adicionar b 2 nos dois lados

x 2 - 2 3 x + 3 2 + y 2 = 3 2

x - 3 2 + y 2 = 3

Agora está mais fácil de visualizar, não é?

Uma circunferência de raio 3 centrada em 3 , 0 .

Agora vamos fazer o mesmo para a outra equação.

x 2 + y 2 = 6 x

x 2 - 6 x + y 2 = 0

Dessa vez, a = x e se - 2 a b = - 6 x , temos b = 3 .

x 2 - 6 x + 3 2 + y 2 = 3 2

x - 3 2 + y 2 = 9

Assim, vemos que essa circunferência tem raio 3 e está centrado em 3,0 .

Se esboçarmos as curvas no plano, vamos obter

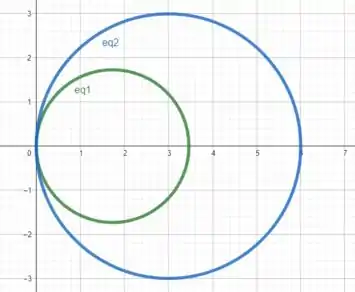
A curva verde é obtida pela equação x - 3 2 + y 2 = 3 , já a azul pela equação x - 3 2 + y 2 = 9 .

Tranquilo até aqui? 😎

Passo 3

Perceba que a área que queremos é a parte que está fora da circunferência verde, mas dentro da circunferência azul.

Como um está circunscrito em outro, podemos dizer que é a área do círculo azul, menos a área do círculo verde.

Em integrais, calculamos a área como

∬ R 1 d R

Vamos converter as coordenadas para polares para facilitar nossa vida aqui.

Temos que escrever d x d y como d r d θ .

Dado que θ = 0 está pontando para o semieixo positivo de x , então vemos que a variação de θ em ambos os casos é dado por π 2 ≤ θ ≤ - π 2 .

Mas e r ? Para converter x e y em r e θ , fazemos que x = r c o s θ e y = r s e n θ , dessa forma x 2 + y 2 = r 2 . Reescrevendo nossas equações como foram dadas no enunciado, temos

x 2 + y 2 = 2 3 x

r 2 = 2 3 r c o s θ

Simplificando...

r = 2 3 c o s θ

Para a outra equação, temos

x 2 + y 2 = 6 x

r 2 = 6 r c o s θ

Simplificando...

r = 6 cos ⁡ θ

Logo, vemos que nossa região R varia entre 6 cos ⁡ θ ≤ r ≤ 2 3 c o s θ

Entendeu essa parte? 😉

Passo 4

Montando nossa integral sem esquecer do jacobiano r , finalmente vamos obter

∫ θ i θ f ∫ r i r f r d r d θ

Substituindo os limites de integração

∫ - π 2 π 2 ∫ 2 3 c o s θ 6 cos ⁡ θ r d r d θ

Integrando r pelo método de integração polinomial

∫ r d r = r 1 + 1 1 + 1 = r 2 2

Aplicando os limites de integração

∫ 2 3 c o s θ 6 cos ⁡ θ r d r = 6 cos ⁡ θ 2 2 - 2 3 c o s θ 2 2

Como a b 2 = a 2 b 2

∫ 2 3 c o s θ 6 cos ⁡ θ r d r = 6 2 cos 2 ⁡ θ 2 - 2 3 2 c o s 2 θ 2

∫ 2 3 c o s θ 6 cos ⁡ θ r d r = 36 cos 2 ⁡ θ 2 - 4 · 3 c o s 2 θ 2

∫ 2 3 c o s θ 6 cos ⁡ θ r d r = 36 cos 2 ⁡ θ 2 - 12 c o s 2 θ 2

Simplificando...

∫ 2 3 c o s θ 6 cos ⁡ θ r d r = 24 cos 2 ⁡ θ 2 = 12 c o s 2 θ

Continuando a integral, vamos obter

∫ - π 2 π 2 12 c o s 2 θ d θ = 12 ∫ - π 2 π 2 c o s 2 θ d θ

Bacana, não é? 🤩

Passo 5

A integral de c o s 2 θ é obtida aplicando uma relação trigonométrica que diz

c o s 2 θ = 1 + cos ⁡ 2 θ 2

Ou seja

∫ c o s 2 θ d θ = ∫ 1 + cos ⁡ 2 θ 2 d θ = 1 2 ∫ 1 + cos ⁡ 2 θ d θ

∫ c o s 2 θ d θ = 1 2 ∫ 1 d θ + ∫ cos ⁡ 2 θ d θ

Substituindo 2 θ por u , vamos obter que d u d θ = 2 , ou seja, d θ = d u 2 .

A integral de uma constante é dada por

∫ 1 d θ = 1 · θ = θ

Já a integral de cos ⁡ 2 θ plicando o método de substituição

∫ cos ⁡ 2 θ d θ = ∫ cos ⁡ u 2 d u

Essa integral deve ser conhecida e é igual a

∫ cos ⁡ u 2 d u = s e n u 2

Substituindo u por 2 θ

∫ cos ⁡ 2 θ d θ = s e n 2 θ 2

∫ c o s 2 θ d θ = 1 2 ∫ 1 d θ + ∫ cos ⁡ 2 θ d θ

∫ c o s 2 θ d θ = 1 2 θ + s e n 2 θ 2

Aplicando os limites de integração

∫ - π 2 π 2 c o s 2 θ d θ = 1 2 π 2 + s e n 2 π 2 2 - 1 2 - π 2 + s e n 2 - π 2 2

∫ - π 2 π 2 c o s 2 θ d θ = 1 2 π 2 + s e n π 2 - 1 2 - π 2 + s e n - π 2

Como s e n π = 0 , temos

∫ - π 2 π 2 c o s 2 θ d θ = 1 2 π 2 + 0 2 - 1 2 - π 2 + 0 2

Organizando um pouco mais

∫ - π 2 π 2 c o s 2 θ d θ = π 4 + π 4 = π 2

Logo, temos que

∫ - π 2 π 2 ∫ 2 3 c o s θ 6 cos ⁡ θ r d r d θ = 12 ∫ - π 2 π 2 ∫ 2 3 c o s θ 6 cos ⁡ θ r d r d θ

∫ - π 2 π 2 ∫ 2 3 c o s θ 6 cos ⁡ θ r d r d θ = 12 π 2

∫ - π 2 π 2 ∫ 2 3 c o s θ 6 cos ⁡ θ r d r d θ = 6 π

Portanto, a área delimitada pela região R é igual a 6 π !

Fim! Iae, o que achou? Responde Aí! 😁

Resposta

∫ - π 2 π 2 ∫ 2 3 c o s θ 6 cos ⁡ θ r d r d θ = 6 π

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}