Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 105123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule a área da região plana entre as retas 3 y = 3 x , y = 3 x e limitada por x 2 + y 2 = 2 x .

Passo 1

Quando um determinado problema nos pede a área de uma região, o que ele está querendo na verdade é que calculemos a seguinte integral

∬ D 1 d A  

Onde D , é justamente a nossa região ;)

Passo 2

Se a gente quer a área de uma região, nada melhor do que começar entendendo melhor sobre essa região, certo?! Então bora!

Ela é formada, para começo de conversa, pela curva x 2 + y 2 = 2 x , que não parece, mas é uma circunferência, veja só...

x 2 + y 2 = 2 x     →       x 2 - 2 x + y 2 = 0

Completando quadrado para eliminar esse 2 x ...

x 2 - 2 x + y 2 = 0     →     x - 1 2 - 1 + y 2 = 0     →     x - 1 2 + y 2 = 1

Viram só?! É uma circunferência de raio 1 e deslocada 1 unidade a direita no eixo x , dessa forma aqui

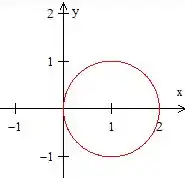
A região também está delimitada por duas retas que passam pela origem, y = 3 3 x e y = 3 x .

Juntando tudo vamos ver que a nossa região é

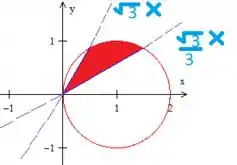
Passo 3

Como estamos trabalhando com uma região dentro de uma circunferência, será legal se fizermos uma mudança para coordenadas polares

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

Onde θ varia da reta y = 3 3 x até a reta y = 3 x , ou seja... substituindo nossas novas variáveis...

y = 3 3 x     →     r sin ⁡ θ = 3 3   r cos ⁡ θ     →     sin ⁡ θ = 3 3   cos ⁡ θ   → sin ⁡ θ cos ⁡ θ = 3 3       → tan ⁡ θ = 3 3 →

θ m i n = arctan ⁡ 3 3 = π 6

E o ângulo máximo ...

y = 3 x   →   r sin ⁡ θ = 3   r cos ⁡ θ   →   sin ⁡ θ cos ⁡ θ = 3     →   tan ⁡ θ = 3     →

θ m á x = arctan ⁡ 3 = π 3

Logo, concluímos que o nosso θ varia...

θ m á x ≤ θ ≤ θ m i n       →     π 6 ≤ θ ≤ π 3

Passo 4

Para a gente encontrar os limites de r , vamos substituir as coordenas na equação da circunferência que é quem delimita o nosso raio.

x 2 + y 2 = 2 x       →       r cos ⁡ θ 2 + r sin ⁡ θ 2 = 2 r cos ⁡ θ   →   r 2 c o s 2 θ + s i n 2 θ = 2 r cos ⁡ θ →

r 2 = 2 r cos ⁡ θ → r = 2 cos ⁡ θ    

Onde concluímos que o raio varia de

0 ≤ r ≤ 2 cos ⁡ θ

Passo 5

Agora basta a gente montar nossa integral iterada substituindo os limites da nossa região e ser feliz;)

Ahhhh! E a gente não pode se esquecer de que quando realizamos uma mudança de coordenadas, devemos multiplicar a nossa função pelo jacobiano, okay?

∬ D 1 d x d y = ∫ π 6 π 3 ∫ 0 2 cos ⁡ θ 1   .     J   d r d θ = ∫ π 6 π 3 ∫ 0 2 cos ⁡ θ r   d r d θ →

∫ π 6 π 3 ∫ 0 2 cos ⁡ θ r   d r d θ = ∫ π 6 π 3 r 2 2 0 2 cos ⁡ θ d θ = ∫ π 6 π 3 ( 2 cos ⁡ θ ) 2 2 d θ = ∫ π 6 π 3 4   c o s 2 θ 2 d θ =

2 ∫ π 6 π 3 c o s 2 θ   d θ

Lembrando da nossa identidade trigonométrica c o s 2 θ = 1 + cos ⁡ ( 2 θ ) 2 ficaremos...

2 ∫ π 6 π 3 c o s 2 θ   d θ = 2 ∫ π 6 π 3 1 + cos ⁡ 2 θ 2 d θ =   ∫ π 6 π 3 1 + cos ⁡ 2 θ   d θ =

θ + sin ⁡ 2 θ 2 π 6 π 3 = π 3 + sin ⁡ 2 π 3 2 - π 6 + sin ⁡ 2 π 6 2 = π 3 + 3 4 - π 6 - 3 4

Logo

∬ D 1 d x d y = π 3 - π 6 = π 6

Resposta

Á r e a = π 6

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}