Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 111123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere S a região do plano acima da reta y = x dentro do círculo x 2 + y - 1 2 = 1 .

  1. Escreva ∬ S   5 x 3   d A em integrais iteradas em coordenadas cartesianas e em coordenadas polares.
  2. Escolha uma das formas encontradas no item anterior para mostrar que ∬ A   5 x 3   d A = - 5 12 .

Passo 1

Item a) pois então, vamos começar a destrinchar esse problema entendendo um pouco mais sobre a superfície S .

A gente já sabe quem é a reta y = x , e sabemos também que x 2 + ( y - 1 ) 2 = 1 é um círculo. Porém que espécie de círculo é esse? Bem... ele é um círculo deslocado uma unidade pra cima no eixo y . :)

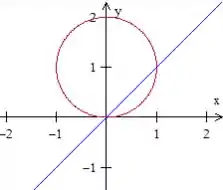
Bem, a superfície S é essa que está acima da reta y = x em azul

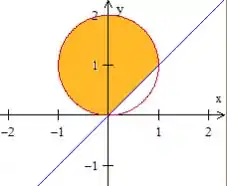
Passo 2

Repare que pra gente escrever essa região em coordenadas cartesianas, temos que descreve-la do tipo 1 . Mas note também que para descrever essa região do tipo 1, temos que dividir essa região em dois pedaços

Parte A

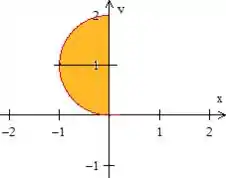
Parte B

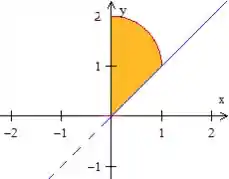
Passo 3

Vamos começar então, descrevendo como região do tipo 1 a parte A :

  • x varia em um intervalo numérico bem definido, que no nosso caso é de - 1 até a origem, ou seja

    • - 1 ≤ x ≤ 0

  • Pra gente olhar y , a gente vai pegar uma reta paralela ao eixo y e observar onde essa reta entra na região A :

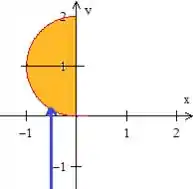
    • Note que essa reta, em azul, ela entra na região na parte de baixo da circunferência. E que equação tem essa parte?

    Bem, se a gente busca algo em função de y , é legal isolar y na equação do círculo

    x 2 + ( y - 1 ) 2 = 1

    y - 1 2 = 1 - x 2

    Jogando esse ao quadrado pro outo lado mais ou menos raiz...

    y = 1 ± 1 - x 2

    Logo y entra na parte de baixo, com raiz negativa, e sai na parte de cima, com raiz positiva, ou seja

    1 - 1 - x 2 ≤ y ≤ 1 + 1 - x 2

    Essa descrição da região A , nos gera a primeira integral iterada que precisamos

    ∬ A   5 x 3   d A = ∫ - 1 0 ∫ 1 - 1 - x 2 1 + 1 - x 2 5 x 3   d A

    Passo 4

    Ainda falta descrever a parte B . Então vamos lá!

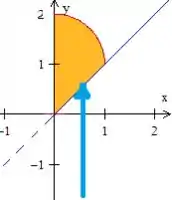
  • x varia no seu intervalo numérico bem definido, mas agora a gente está descrevendo B , então 0 ≤ x ≤ 1 .
  • Pra y , vamos novamente utilizar a ajuda de uma reta paralela a ao eixo y

Note que y agora varia da reta, até a parte de cima da circunferência (aquela equação que tem a raiz positiva), ou seja

x ≤ y ≤ 1 + 1 - x 2

Montando a integral iterada da parte B

∬ B   5 x 3   d A = ∫ 0 1 ∫ x 1 + 1 - x 2 5 x 3   d A

Passo 4

Pois então, a gente não quer a integral em A e nem B , mas a gente quer em A e B ao mesmo tempo, pois a união das duas é a região S do problema, ou seja,

∬ S   5 x 3   d A = ∬ A   5 x 3   d A + ∬ B   5 x 3   d A

∬ S   5 x 3   d A = ∫ - 1 0 ∫ 1 - 1 - x 2 1 + 1 - x 2 5 x 3   d A + ∫ 0 1 ∫ x 1 + 1 - x 2 5 x 3   d A

Passo 5

Poxa vida! Que probleminha grande! Sim, concordo, mas não vamos desistir do nosso ponto :)

Vamos então, escrever essa mesma região em coordenas polares, ou seja...

x = r cos ⁡ θ

y = r sen ⁡ θ

x 2 + y 2 = r 2

J = r

O bom dessa de descrever a região em coordenadas polares, é que não precisa de dividir a região em duas, a única coisa que temos que fazer é descrever a variação das novas variáveis.

Passo 6

Observe que o limite mínimo do raio r é a origem, e o limite máximo está em cima da circunferência, logo, devemos substituir essas novas coordenadas na equação da circunferência:

x 2 + y - 1 2 = 1

Fatorando esse quadrado aí

x 2 + y 2 - 2 y + 1 = 1

x 2 + y 2 = 2 y

Agora substituindo os elementos das coordenadas polares

r 2 = 2   r sen ⁡ θ

r = 2   sen ⁡ θ

Logo

0 ≤ r ≤ 2   sen ⁡ θ

Quanto ao ângulo θ , a gente pode notar que ele varia da reta azul até o ângulo π , correto?

E o que significa ele começara a variar da reta y = x ? Que ângulo é esse?

Bem, um bizu pra gente descobrir esse ângulo aí é lembrar de que essa reta é a bissetriz do plano X Y , logo o ângulo que ele faz com o eixo x é de 45° ou π 4 !!!:)

π 4 ≤ θ ≤ π

Agora montando a integral substituindo a função também... AHH! Não esqueça de multiplicar pelo jacobiano!

∬ S   5 x 3   d A = ∫ π 4 π ∫ 0 2 sen ⁡ θ 5 r cos ⁡ θ 3 .   J   d r d θ

∬ S   5 x 3   d A = 5 ∫ π 4 π ∫ 0 2 sen ⁡ θ r 4 cos 3 ⁡ θ   d r d θ

Passo 7

Item b) agora é só escolher uma dessas integrais aí e correr para um abraço! Vamos pegar esse último aí, ok? Menos contas! :)

Integrando primeiro em r e tomando θ constante

∬ S   5 x 3   d A = 5 ∫ π 4 π cos 3 ⁡ θ r 5 5 0 2 sen ⁡ θ d θ

Substituindo os imites em r

∬ S   5 x 3   d A = 5 ∫ π 4 π cos 3 ⁡ θ 2 5 . sen 5 ⁡ θ 5 d θ

Simplificando essa expressão tirando esse 5 de baixo e tal...

∬ S   5 x 3   d A = ∫ π 4 π 32  cos 3 ⁡ θ sen 5 ⁡ θ d θ

Agora vamos fazer o seguinte: colocar um dos cossenos próximo do d θ sobrando apenas o cos 2 ⁡ θ   que a gente vai substituir por cos 2 ⁡ θ = 1 - sen 2 ⁡ θ da identidade fundamental

∬ S   5 x 3   d A = ∫ π 4 π 32  cos 2 ⁡ θ sen 5 ⁡ θ cos ⁡ θ d θ

∬ S   5 x 3   d A = 32 ∫ π 4 π 1 - sen 2 ⁡ θ sen 5 ⁡ θ cos ⁡ θ d θ

∬ S   5 x 3   d A = 32 ∫ π 4 π ( sen 5 ⁡ θ - sen 7 ⁡ θ ) cos ⁡ θ d θ

Repare que cos ⁡ θ é a derivada do seno, logo a gente pode fazer uma substituição do tipo

u = sen ⁡ θ       ⇒           d u = cos ⁡ θ d θ

Não podemos esquecer de mudar também os limites, ou seja, Quanto teta assumi π 4 , u = sen ⁡ π 4 = 2 2 . Quando θ = π , u = sen ⁡ π = 0 ... Logo

∬ S   5 x 3   d A = 32 ∫ 2 2 0 u 5 - u 7 d u

∬ S   5 x 3   d A = 32 u 6 6 - u 8 8 2 2 0

Substituindo os limites de integração

∬ S   5 x 3   d A = - 32 2 2 6 6 - 2 2 8 8 = - 32 2 3 2 6 6 - 2 4 2 8 8

Simplificando essas continhas aí

∬ S   5 x 3   d A = - 32 2 - 3 6 - 2 - 4 8 = - 32 1 6 × 8 - 1 16 × 8

- 4 6 + 4 16 = - 5 12

Resposta

Item a)

∬ S   5 x 3   d A = ∫ - 1 0 ∫ 1 - 1 - x 2 1 + 1 - x 2 5 x 3   d A + ∫ 0 1 ∫ x 1 + 1 - x 2 5 x 3   d A

E

∬ S   5 x 3   d A = 5 ∫ π 4 π ∫ 0 2 sen ⁡ θ r 4 cos 3 ⁡ θ   d r d θ

Item b)

∬ S   5 x 3   d A = - 5 12

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}