Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 130123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFSCAR, Sem Campus, Cálculo 3, Listas de C3 - Profª Alessandra Verri - Lista 3, Questão 1d

Exercício 1. Por meio de coordenadas polares, calcule a integral

d) ∫ - a a ∫ 0 a 2 - x 2 e - x 2 + y 2 d y d x

Passo 1

Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nesse problema queremos calcular a integral ∫ - a a ∫ 0 a 2 - x 2 e - x 2 + y 2 d y d x em que a região limitada por 0 ≤ y ≤ a 2 - x 2 e - a ≤ x ≤ a . Pra isso temos que usar coordenadas polares!

Tem ideia de como fazer isso? 🤔

Fazemos esse tipo de conversão quando temos alguma simetria polar na região de integração ou na função de integração da integral.

Para fazer a conversão de coordenadas cartesianas para coordenadas polares temos que fazer x = r cos ⁡ θ e y = r sin ⁡ θ .

Para completar a conversão, multiplicamos a função de integração por r e definimos os limites de integração em função de r e θ .

Bacana, não é? Bora começar! 😉

Passo 2

Vamos começar convertendo nossa função de integração...

f x , y = e - x 2 + y 2

Fazendo x = r cos ⁡ θ e y = r sin ⁡ θ .

f r , θ = e - r cos ⁡ θ 2 + r sin ⁡ θ 2

f r , θ = e - r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ

f r , θ = e - r 2 cos 2 ⁡ θ + sin 2 ⁡ θ

Como cos 2 ⁡ θ + sin 2 ⁡ θ = 1 ...

f r , θ = e - r 2

f r , θ = e - r 2

Agora temos que definir os limites de integração para as variáveis polares r e θ ...

No caso, y varia de 0 a a 2 - x 2 , ou seja, estamos interessados na parte superior da circunferência de raio a .

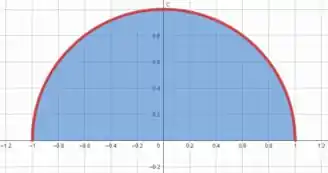
Isso implica que θ varia de 0 a π .

Já como x varia de - a a a , podemos perceber que r varia de 0 a a .

Tranquilo até aqui? 😉

Passo 3

Montando nossa integral em coordenadas polares, temos que

∫ - a a ∫ 0 a 2 - x 2 e - x 2 + y 2 d y d x → ∫ 0 π ∫ 0 a e - r 2 · r d r d θ

∫ 0 π ∫ 0 a r e - r 2 d r d θ

Integrando com relação a r pelo método de substituição...

∫ r e - r 2 d r = - 1 2 e - r 2

Aplicando os limites de integração

∫ 0 a r e - r 2 d r = - 1 2 e - a 2 - - 1 2 e - 0 2

∫ 0 a r e - r 2 d r = 1 2 1 - e - a 2

Integrando o resultado em função de θ

∫ 1 2 1 - e - a 2 d θ = 1 2 1 - e - a 2 θ

E por fim aplicando os limites de integração

∫ 0 π 1 2 1 - e - a 2 d θ = 1 2 1 - e - a 2 π - 1 2 1 - e - a 2 0

∫ 0 π 1 2 1 - e - a 2 d θ = 1 - e - a 2 π 2

Com isso temos que

∫ - a a ∫ 0 a 2 - x 2 e - x 2 + y 2 d y d x = 1 - e - a 2 π 2

Fim! Iae, o que achou? Responde Aí! 😁

Resposta

∫ - a a ∫ 0 a 2 - x 2 e - x 2 + y 2 d y d x = 1 - e - a 2 π 2

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}