Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 110123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

  1. Passe para coordenadas polares e calcule:

∫ 0 1 ∫ 1 - 1 - y 2 1 + 1 - y 2 x y   d x d y

Passo 1

Bem, a primeira coisa aqui é tentar entender um pouco melhor sobre a própria região que estamos querendo trabalhar.

A única informação que temos sobre a região é dada pela própria integral afinal de contas sabemos que:

0 ≤ y ≤ 1

Pow! Com essa primeira inequação, ganhamos:

y = 0

y = 1

Colocando as duas primeiras equações em um plano obtemos essas duas retas paralelas a o X :

Passo 2

Como x está na integral de dentro, sabemos então que o limite de dentro é dele, veja:

1 - 1 - y 2 ≤ x ≤ 1 + 1 - y 2

Em relação a essas duas outras igualdades tiramos... x = 1 - 1 - y 2

x = 1 + 1 - y 2

Observe que é difícil de enxergar que curvas são essas dessa forma. Por isso a ideia é justamente tirar essa raiz feia aí, observe:

x - 1 = - 1 - y 2           →               x - 1 2 = 1 - y 2

x - 1 = + 1 - y 2             →               x - 1 2 = 1 - y 2

Note que em ambas as equações, chagamos em um mesmo resultado : Isso normalmente acontece quando estamos trabalhando com circunferências, se lembra? E olha que legal

x - 1 2 = 1 - y 2                   ⇒ P a s s a n d o   o   y   p a r a   o   o u t r o   l a d o …                     x - 1 2 + y 2 = 1

RA!!! É de fato uma circunferência de raio 1 (porém ela está uma unidade a direita ):

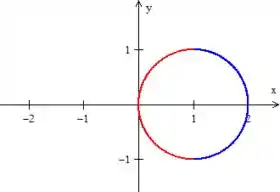
FIQUE LIGADO: Esse lado negativo do x em x = 1 - 1 - y 2 era apenas para indicar que estávamos separando a circunferência em duas partes e essa era a do lado esquerdo (vermelha), sacou?

Passo 3

Wooooow! Cuidado, pois ainda não terminamos de ver a região! Temos que colocar essas coisas juntas:

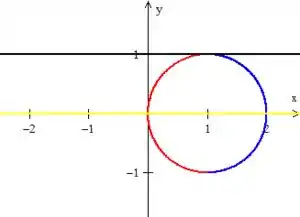
Assim, a região é...

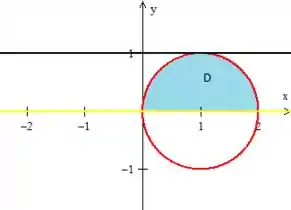
Passo 4

Como o próprio problema nos pediu, devemos mudar então para as famosas coordenadas polares, onde vamos fazer a seguinte troca:

x = r cos ⁡ θ

y = r sin ⁡ θ

x 2 + y 2 = r 2

Não se esqueça do Jacobiano:

J = r

Pois bem! Toda e qualquer mudança que fazemos temos que determinar quais são os limites dos novos camaradas (no caso é o r e θ ). Bora?

Passo 5

Para o limite de θ , esse é bem simples, afinal, basta que olhemos para a região que estamos trabalhando. Lembrando que θ é o ângulo que gira no sentido anti-horário partindo daqui:

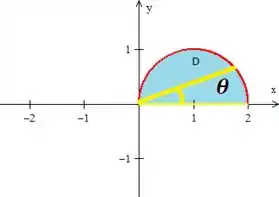
Então nesse caso, esse ângulo dá uma meia volta:

0 ≤ θ ≤ π 2

Quanto ao limite do raio, bem, sabemos que o raio varia da origem, até a curva vermelha

0 ≤ r ≤ C u r v a   V e r m e l h a

Como a curva vermelha tem equação x - 1 2 + y 2 = 1 em termos de x e y , precisamos substituir as mudanças polares, mas antes...

x - 1 2 + y 2 = 1           →             x 2 - 2 x + 1 + y 2 = 1         →

x 2 + y 2 = 2 x

Substituindo agora

r 2 = 2 ∙ r cos ⁡ θ         →               r = 2 cos ⁡ θ

Logo

0 ≤ r ≤ C u r v a   V e r m e l h a

0 ≤ r ≤ 2 cos ⁡ θ

Passo 6

Com esses dados de variação em mãos

0 ≤ r ≤ 2 cos ⁡ θ

0 ≤ θ ≤ π 2

podemos então agora montar a integral simplesmente substituindo tudo (não esqueça de multiplicar pelo Jacobiano quando realizar a troca)

∫ 0 1 ∫ 1 - 1 - y 2 1 + 1 - y 2 x y   d x d y = ∫ 0 π 2 ∫ 0 2 cos ⁡ θ r cos ⁡ θ r sin ⁡ θ ∙ J   d r d θ =

∫ 0 π 2 ∫ 0 2 cos ⁡ θ r 3 cos ⁡ θ   sin ⁡ θ d r d θ

Agora é só integrar! Bora?

Passo 7

Calculando primeiro a integral de dentro

∫ 0 π 2 ∫ 0 2 cos ⁡ θ r 3 cos ⁡ θ   sin ⁡ θ d r d θ = ∫ 0 π 2 ∫ 0 2 cos ⁡ θ r 3 cos ⁡ θ   sin ⁡ θ d r d θ

Como aquele produto entre seno e cosseno são constantes perante o r , eles vazam da integral de dentro

∫ 0 π 2 cos ⁡ θ   sin ⁡ θ ∫ 0 2 cos ⁡ θ r 3 d r d θ =

∫ 0 π 2 cos ⁡ θ   sin ⁡ θ r 4 4 0 2 cos ⁡ θ d θ =

substituindo os limites...

∫ 0 π 2 cos ⁡ θ   sin ⁡ θ 2 cos ⁡ θ 4 4 d θ =

simplificando um pouco...

4 ∫ 0 π 2 sin ⁡ θ cos ⁡ θ 5 d θ

Pra resolver essa integral aí, basta fazermos uma substituição simples. Veja!

cos ⁡ θ = t

d t = - sin ⁡ θ d θ               →         sin ⁡ θ d θ = - d t

antes de substituir, não se esqueça dos limites, heim!

θ = 0                     →                           t = cos ⁡ 0 = 1

θ = π 2                     →                           t = cos ⁡ π 2 = 0

4 ∫ 0 π 2 sin ⁡ θ cos ⁡ θ 5 d θ =

4 ∫ 1 0 - t 5   d t

Lembre-se que se invertermos esses limites de integração o sinal da integral muda:

4 ∫ 1 0 - t 5   d t = 4 ∫ 0 1 t 5   d t =

4 t 6 6 0 1 =

finalmente...

2 3

Resposta

2 3

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}