Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 117123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passe para coordenadas polares e calcule:

∫ 0 1 ∫ x 2 2 - x 2 x 2 + y 2 d y d x

Passo 1

Aqui ele já é bem direto, temos que passar pra coordenadas polares. Vamos lembrar como que fica:

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

A integral vai ficar, então:

∬ D x 2 + y 2 d x d y = ∬ Q r 2 r d r d θ

⇒ ∬ Q r 2 d r d θ

Só temos que ver como que vai ficar esse novo domínio Q pra podermos calcularmos logo.

Passo 2

Vamos fazer o esboço da região pra entendermos melhor.

Temos uma semicircunferência de raio 2 e y ≥ 0 e uma parábola y = x 2 . Com 0 ≤ x ≤ 1 , ficamos com a região laranjinha abaixo:

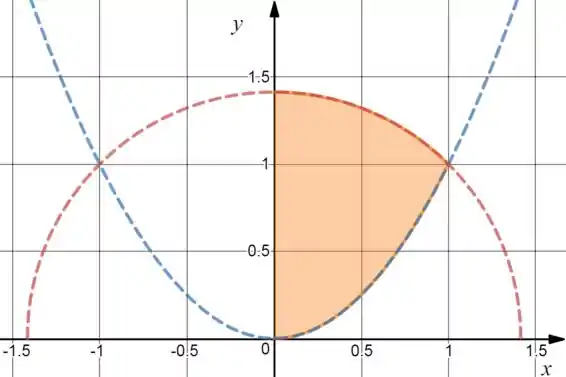
O θ é fácil de ver, vai de 0 a π / 2 . O r começa 0 , e varia dependendo de θ , mas não dá pra escrever isso em uma equação só, então vamos ter que separar em dois pedaços.

O ponto que os dois gráficos se encontram é o ponto 1,1 , que tem θ = π / 4 , então vamos ter duas integrais:

∬ Q r 2 r d r d θ = ∫ 0 π 4 ∫ 0 g θ r 2 d r d θ + ∫ π 4 π 2 ∫ 0 h θ r 2 d r d θ

Vamos ver como que ficam essas funções g θ e h θ !

Passo 3

O primeiro pedaço era aquele da parábola:

y = x 2 → r sen ⁡ θ = r 2 cos 2 ⁡ θ

⇒ r = sen ⁡ θ cos 2 ⁡ θ

Então vamos integrar:

∫ 0 π 4 ∫ 0 sen ⁡ θ cos 2 ⁡ θ r 2 d r d θ = ∫ 0 π 4 r 3 3 │ 0 sen ⁡ θ cos 2 ⁡ θ d θ

⇒ 1 3 ∫ 0 π 4 sen ⁡ θ cos 2 ⁡ θ 3 d θ

Essa integral parece bem chatinha de calcular, hein? Mas vamos tentar dar um jeito...

1 3 ∫ 0 π 4 sen 3 ⁡ θ cos 6 ⁡ θ d θ = 1 3 ∫ 0 π 4 sen ⁡ θ sen 2 ⁡ θ cos 6 ⁡ θ d θ

⇒ 1 3 ∫ 0 π 4 1 - cos 2 ⁡ θ cos 6 ⁡ θ sen ⁡ θ d θ

Agora a gente faz uma substituição:

u = cos ⁡ θ → d u = - sen ⁡ θ d θ

Então vamos ficar com:

1 3 ∫ 1 - cos 2 ⁡ θ cos 6 ⁡ θ sen ⁡ θ d θ ⏟ - d u = - 1 3 ∫ 1 - u 2 u 6 d u

⇒ - 1 3 ∫ 1 u 6 d u - ∫ u 2 u 6 d u

⇒ - 1 3 ∫ u - 6 d u - ∫ u - 4 d u

⇒ - 1 3 u - 5 - 5 - u - 3 - 3 = - 1 3 1 3 cos 3 ⁡ θ - 1 5 cos 5 ⁡ θ

Aplicando os limites de integração:

- 1 3 1 3 cos 3 ⁡ θ - 1 5 cos 5 ⁡ θ θ = 0 θ = π 4 = - 1 3 1 3 2 2 3 - 1 5 2 2 5 - 1 3 - 1 5  

= - 1 3 8 6 2 - 32 20 2 - 2 15 = - 1 3 - 2 2 15 - 2 15 = 2 2 + 2 45

Ufa... Espero que o outro pedaço seja mais tranquilo, né?

Passo 4

Vamos ver o segundo pedaço, que é o da semicircunferência:

y = 2 - x 2 → y 2 + x 2 = 2

⇒ r 2 = 2 → r = 2

O que é bem mais tranquilo, né? Haha

Vamos ficar então com:

��� π 4 π 2 ∫ 0 2 r 2 d r d θ = ∫ π 4 π 2 r 3 3 │ 0 2 d θ

⇒ 1 3 ∙ 2 2 ∙ θ │ π 4 π 2 = 2 2 3 ∙ π 2 - π 4 = 2 π 6

Passo 5

Somando os dois pedaços, a gente tem:

∬ Q r 2 r d r d θ = ∫ 0 π 4 ∫ 0 sen ⁡ θ cos 2 ⁡ θ r 2 d r d θ + ∫ π 4 π 2 ∫ 0 2 r 2 d r d θ

⇒ 2 2 + 2 45 + 2 π 6

Pronto, foi!

Resposta

2 2 + 2 45 + 2 π 6

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}