Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 108123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

  1. Passe para coordenadas polares e calcule:

∫ 0 3 ∫ 0 9 - x 2 arctan ⁡ y x   d y d x

Passo 1

Bem, a primeira coisa aqui é tentar entender um pouco melhor sobre a própria região que estamos querendo trabalhar.

A única informação que temos sobre a região é dada pela própria integral afinal de contas sabemos que:

0 ≤ x ≤ 3

0 ≤ y ≤ 9 - x 2

Pow! Com essa primeira inequação, ganhamos:

x = 0

x = 3

Colocando as duas primeiras equações em um plano obtemos essas duas retas paralelas a o Y :

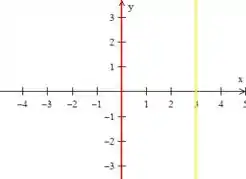
Passo 2

Com a outra informação tirada da integral...

0 ≤ y ≤ 9 - x 2

tiramos que... y = 0

y = 9 - x 2

A primeira equação é easy de desenhar, pois ela é o próprio eixo x :

Quanto à segunda, observe que é difícil de enxergar que curva é essa dessa forma. Por isso a ideia é justamente tirar essa raiz feia aí, observe:

y = 9 - x 2                 →               y 2 = 9 - x 2

y 2 + x 2 = 9

RA!!! É uma circunferência de raio 3 !

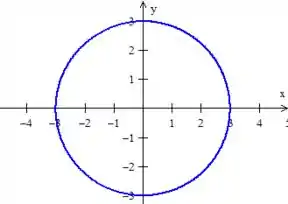
Porém, cuidado! Só queremos o lado positivo de y , então...

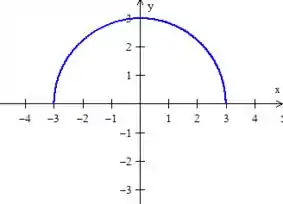
Passo 3

Dessa forma já é possível notar qual região estamos trabalhando juntando todas essas curvas dos passos anteriores:

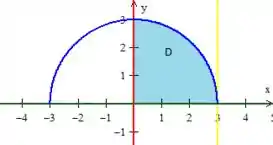
Passo 4

Como o próprio problema nos pediu, devemos mudar então para as famosas coordenadas polares, onde vamos fazer a seguinte troca:

x = r cos ⁡ θ

y = r sin ⁡ θ

Não se esqueça do Jacobiano:

J = r

Pois bem! Toda e qualquer mudança que fazemos temos que determinar quais são os limites dos novos camaradas (no caso é o r e θ ). Bora?

Passo 5

Encontrar a variação desse caras é muito fácil pra gente, pois o θ está indo até 90 ° partindo da origem:

0 ≤ θ ≤ π 2

Enquanto que o r sai da origem e vai até a borda que tem raio 3 ...

0 ≤ r ≤ 3

Passo 6

Antes de substituirmos tudo na integral,

∫ 0 3 ∫ 0 9 - x 2 arctan ⁡ y x   d y d x

repare que é fundamental a gente trocar esse arco tangente aí pelas coordenas polares. Mas cara! Com a substituição polar que fizemos, o ângulo θ é esse daqui, ohh:

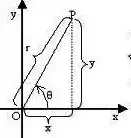
Logo, tangente desse ângulo sempre será y x , certo?

tan ⁡ θ = y x

Portanto podemos falar que o arco cuja tangente é y x , é o ângulo θ , sacou? Veja:

θ = arctan ⁡ y x

∫ 0 3 ∫ 0 9 - x 2 arctan ⁡ y x   d y d x

Sabendo disso, podemos então agora montar a integral simplesmente substituindo tudo (não esqueça de multiplicar pelo Jacobiano quando realizar a troca)

∫ 0 3 ∫ 0 9 - x 2 arctan ⁡ y x   d y d x = ∫ 0 π 2 ∫ 0 3 θ ∙ J   d r d θ =

∫ 0 π 2 ∫ 0 3 θ ∙ r   d r d θ

Agora é só integrar! Bora?

Passo 7

Resolvendo então a integral de dentro...

∫ 0 π 2 ∫ 0 3 θ ∙ r   d r d θ = ∫ 0 π 2 ∫ 0 3 θ ∙ r   d r d θ

Como θ independe da variável que este se integrando dentro, ele pode vazar dessa primeira integral:

∫ 0 π 2 ∫ 0 3 θ ∙ r   d r d θ = ∫ 0 π 2 θ ∫ 0 3 r   d r d θ =

∫ 0 π 2 θ r 2 2 0 3 d θ

substituindo

∫ 0 π 2 θ 3 2 2 d θ = 9 2 ∫ 0 π 2 θ d θ =

Integrando novamente...

9 2 θ 2 2 0 π 2 =

9 π 2 16

Resposta

d )       9 π 2 16

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}