Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 431234567891011121314151617181920212223242526272829303132333435363738394041424445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 2: Considere as regiões do espaço

U 1 = x ,   y ,   z ∈ R 3   |   z 2 ≤ x 2 + y 2 + 3 ,     z ≥ 0

U 2 = x ,   y ,   z ∈ R 3   |   z ≥ x 2 + y 2 + 1

Seja U = U 1 ∩ U 2 .

  1. Esboce hachurando U ∩ x = 0 .
  2. Considere V = U ∩ x ≥ 0

    3. Escreva V o l V , na forma de uma integral iterada, usando obrigatoriamente coordenadas polares.

  3. Calcule V o l V .

Passo 1

a )

Então, nesse primeiro item, o que o problema nos pede é basicamente a intersecção da nossa região U com o plano x = 0 . Então primeiro a gente deve saber bem quem é a região U , por isso essa é a nossa primeira tarefa: desenhar U !

Veja que a U é a intersecção de outras duas superfícies:

U 1 = x ,   y ,   z ∈ R 3   |   z 2 ≤ x 2 + y 2 + 3 ,     z ≥ 0

U 2 = x ,   y ,   z ∈ R 3   |   z ≥ x 2 + y 2 + 1

Com elas, tiramos duas igualdades que são bem conhecidas:

1 º )         z 2 = x 2 + y 2 + 3

2 º )         z = x 2 + y 2 + 1

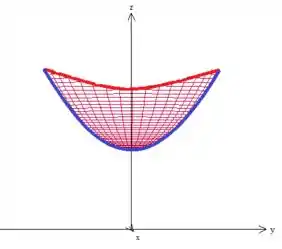
A primeira nos representa um hiperboloide de duas folhas que passa por z = ± 3 , porém, como queremos apenas a parte onde z ≥ 0 , o nosso U 1 será:

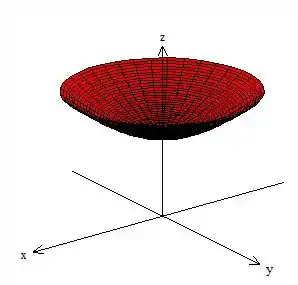
Enquanto isso, temos a segunda que é um paraboloide que está um pouco abaixo do hiperboloide, passando por z = 1 ...

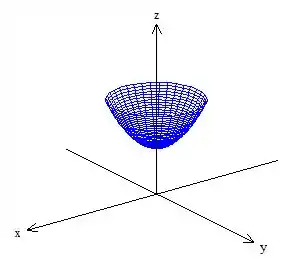
Então esse daqui é o nosso sólido U :

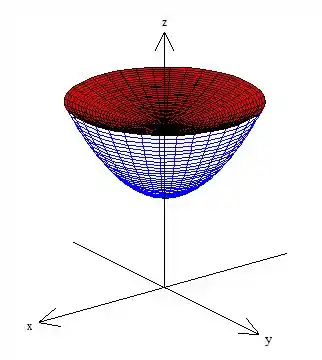
Passo 2

Como queremos a intersecção desses U com o plano x = 0 , basta pegar uma “chapa” no plano z y (esse plano é o plano onde x = 0 )...

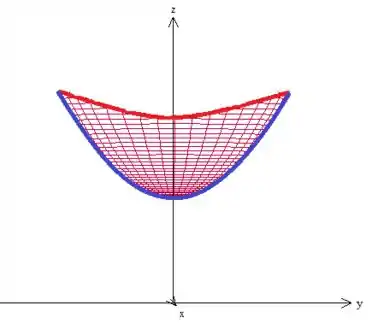
Percebeu? É como se tivesse cortando a região fora e pegando apenas a intersecção !

Passo 3

b )

Agora o problema nos pediu para considerar V , como sendo apenas a região U , mas com x sendo positivo (vamos tirar a parte de trás fora):

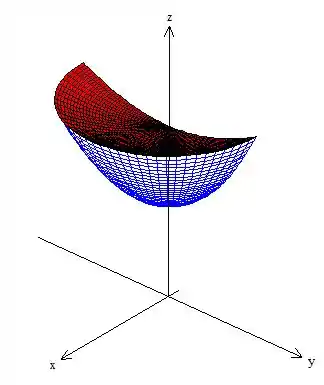
E ele pediu para descrevermos o volume desse novo sólido como uma integral iterada usando as coordenadas polares. Só para ficar claro, volume de sólido é dado pra gente aqui como sendo:

V o l V = ∬ R   f x ,   y - g x ,   y d V

Veja então que temos 2 coisas para fazermos aqui:

1 º ) Encontrar a descrição da região de variação de x e y dentro de R .

2 º )   Encontrar quem são as funções de integração f x ,   y e g x ,   y .

3º) Colocar tanto a região, quanto as funções encontradas em coordenadas polares!

Vamos começar então com a nossa primeira tarefa, vamos nessa!

Passo 4

Para a primeira tarefa, devemos encontrar a variação de x e y dentro do sólido. Bem, para verificar onde eles estão variando, devemos olhar para a projeção do sólido no plano X Y :

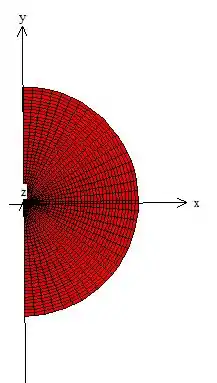
Veja que aparentemente, eles estão dentro desse semicírculo. Para conferirmos se é de fato um semicírculo, vamos definir a equação da circunferência que o delimita, definido pela intersecção entre as duas superfícies:

O limite da projeção é dado na intersecção entre as duas superfícies que formam o sólido:

  z 2 = x 2 + y 2 + 3     z = x 2 + y 2 + 1           →       s u b s t i t u i n d o   a   s e g u n d a   n a   p r i m e i r a   →                                  

z - 1 = x 2 + y 2   �� →         z 2 = z - 1 + 3         →

z 2 - z + 2 = 0

Resolvendo por Báskara...

z 1 = - 1       e         z 2 = 2

Como queremos a parte onde z ≥ 0 ...

z - 1 = x 2 + y 2         →

x 2 + y 2 = 1

OPA! Essa daí é a equação que define o limite na projeção. OU seja, de fato é uma semicircunferência de raio 1 , onde concluímos que a região R de variação de x e y é de fato o semicírculo:

x ,   y ∈ R

Passo 5

A segunda tarefa nos pede para encontrar as funções de integração:

f x ,   y     e   g x ,   y

Como queremos o volume do pedaço que está abaixo do hiperboloide e acima do paraboloide, lembrando que f é sempre a função que esta por cima e a g , a por baixo...

f x ,   y = h i p e r b o l o i d e

g x ,   y = p a r a b o l o i d e

A equação do paraboloide...

  z = g x ,   y = x 2 + y 2 + 1

Já pela equação do hiperboloide...

z 2 = x 2 + y 2 + 3             →                 z = f x ,   y = x 2 + y 2 + 3

Passo 6

Agora devemos passar todas as nossas conquistas do passo 4 e 5 para as coordenadas polares, onde...

x = r cos ⁡ θ

y = r sin ⁡ θ

Não se deve esquecer que o Jacobiano dessa mudança, vale:

J = r

Sempre é bom lembrar também da equação do círculo...

x 2 + y 2 = r 2

Passo 7

No caso, devemos encontrar a nossa região R em coordenadas polares:

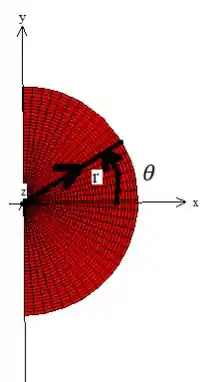
Lembrando que θ é sempre o cara que varia saindo do eixo x girando no sentido positivo, devemos ter que para ele gerar esse semicírculo, ele deve necessariamente começar a girar de - 90 ° até 90 ° ...

- π 2 ≤ θ ≤ π 2

Enquanto isso, r deve iniciar em 0 e ir até o limite que é o raio desse círculo...

0 ≤ r ≤ 1

Passo 8

No caso das funções em coordenadas polares, basta substituir mesmo:

g x ,   y = x 2 + y 2 + 1           →           g r ,   θ = r 2 + 1

f x ,   y = x 2 + y 2 + 3           →           f r ,   θ = r 2 + 3

Passo 9

Então, a integral iterada que representa o volume de V em coordenadas polares é:

V o l V = ∬ R   f x ,   y - g x ,   y d V =

∫ - π 2 π 2 ∫ 0 1 r 2 + 3 - r 2 + 1 ⋅ J d r d θ =

Veja que não podemos esquecer de forma alguma de multiplicar a função pelo Jacobiano ;)

V o l V = ∫ - π 2 π 2 ∫ 0 1 r 2 + 3 - r 2 + 1 ⋅ r d r d θ

Passo 10

c )

Agora é só calcular a integral mesmo:

V o l V = ∫ - π 2 π 2 ∫ 0 1 r 2 + 3 - r 2 + 1 ⋅ r d r d θ

Fazendo uma substituição simples:

r 2 + 3 = u             →               d u = 2 r d r           o u           r d r = d u 2

Não se esquecendo dos limites...

r = 0         →           u = 3

r = 1         →           u = 4

∫ - π 2 π 2 ∫ 0 1 r 2 + 3 - r 2 + 1 ⋅ r d r d θ = ∫ - π 2 π 2 ∫ 3 4 u - u - 2 ⋅ d u 2 d θ =

Integrando em u ...

1 2 ∫ - π 2 π 2 ∫ 3 4 u - u + 2 d u d θ = 1 2 ∫ - π 2 π 2 2 3 u 3 2 - u 2 2 + 2 u 3 4 d θ =

Dando uma simplificada lembrando que u 3 2 = u u ...

1 2 ∫ - π 2 π 2 2 3 u u - u 2 2 + 2 u 3 4 d θ =

1 2 ∫ - π 2 π 2 2 3 ⋅ 4 4 - 4 2 2 + 2 ⋅ 4 - 2 3 ⋅ 3 3 - 3 2 2 + 2 ⋅ 3 d θ =

1 2 ∫ - π 2 π 2 16 3 - 16 2 + 16 2 - 2 3 - 9 2 + 12 2 d θ =

1 2 ∫ - π 2 π 2 16 3 - 2 3 + 3 2 d θ = 8 3 - 3 - 3 4 ∫ - π 2 π 2 d θ =

8 3 - 3 - 3 4 π 2 - - π 2 =

π 23 12 - 3

Resposta

a )

b )   V o l V = ∫ - π 2 π 2 ∫ 0 1 r 2 + 3 - r 2 + 1 ⋅ r d r d θ

c )   π 23 12 - 3

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}