Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 114123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1: Expresse a área do domínio plano dado pelas relações abaixo como uma integral envolvendo coordenadas polares:

x 2 + y 2 ≤ 4 ,                 x 2 + y 2 ≥ 2 y ,                   y ≥ x .

Passo 1

Bem, se o problema nos pediu área de uma região D , então ele só pode estar querendo uma coisa: que calculemos uma integral dupla:

Á r e a   d e   D = ∬ D   1   d A

Para montar a integral, vamos seguir o que se pede e vamos descrever a região que chamamos de D em coordenadas polares, vamos nessa? =)

Passo 2

Mas poxa, ter uma visualização do que é o desenho seria muito interessante não acha? Sempre ajuda mais ! Então vamos lá:

Primeiro, vamos desenhar o círculo de raio 2 : x 2 + y 2 ≤ 4

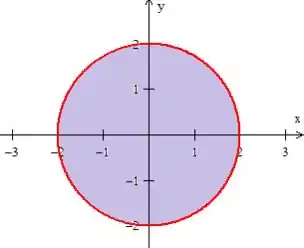
O segundo desenho que vamos fazer agora ( x 2 + y 2 ≥ 2 y ), também é uma circunferência, mas ele tem uma diferença: está deslocado da origem:

x 2 + y 2 ≥ 2 y         →             x 2 + y 2 - 2 y ≥ 0             →

Lembrando que y - 1 2 = y 2 - 2 y + 1

x 2 + y - 1 2 - 1 ≥ 0               →                

x 2 + y - 1 2 ≥ 1

Viu só? Definida por uma circunferência de raio 1 deslocada de 1 unidade da origem em y ...

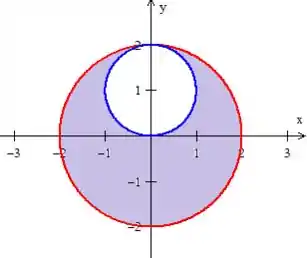
O sinal de maior de maior ou igual é só pra dizer que a gente quer os pontos fora dessa circunferência mesmo, saca?

Beleza! Já desenhamos duas coisas. Sem desânimo vamos desenhar a última...

y ≥ x

y = x é uma reta... O sinal de maior significa que queremos os pontos acima dessa reta:

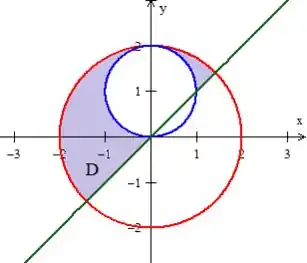
E prontinho!!! Desenho feito com sucesso &

Passo 3

Pow, pra escrever essa região em coordenadas polares, precisamos conhecer bem a mudança que vamos fazer, e essa mudança é essa daqui oh:

x = r cos ⁡ θ

y = r sin ⁡ θ

Juntando essa duas equações, ganhamos outra importante...

x 2 + y 2 = r 2

Quando formos montar a integral, vamos precisar do jacobiano em coordenadas polares, então guarda ele aí:

J = r

Show! Essa é a nossa mudança. Descrever a região nessa mudança é descobrir a variação de r e θ dentro dela, saca? Bora lá!

Passo 4

Dê mais uma olhada com atenção na figura da região:

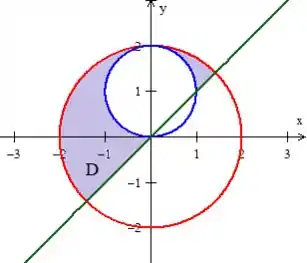
Veja que vamos ter que separar a região D em outras duas partes, pois elas têm configurações diferentes:

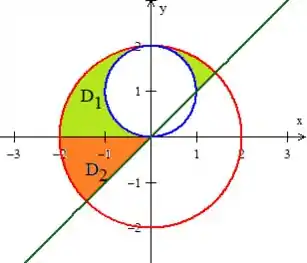
Vamos descrevê-las separadamente então, ok?

Passo 5

Começando pela parte de cima, veja que o ângulo θ , varia da reta verde até 180 ° :

R e t a   V e r d e ≤ θ ≤ π

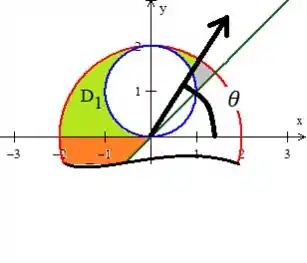
Como a equação da reta verte é y = x , substituindo as polares...

r sin ⁡ θ = r cos ⁡ θ       →       sin ⁡ θ cos ⁡ θ = 1       →

tan ⁡ θ = 1

Como o ângulo está no primeiro quadrante, quem é esse ângulo que tem a tangente igual a 1 ? Isso 45 , então...

R e t a   V e r d e ≤ θ ≤ π           →             π 4 ≤ θ ≤ π

Quanto ao raio r , bem... Ele está entrando na região pela circunferência azul e terminando na vermelha...

C i r c .   A z u l ≤ r ≤ C i r c .   V e r m e l h a

O círculo vermelho tem raio 2 ...

C i r c .   A z u l ≤ r ≤ 2

Quanto a azul, com equação x 2 + y 2 = 2 y ... Nas polares...

x 2 + y 2 = 2 y           →               r 2 = 2   r sin ⁡ θ         →

r = 2 sin ⁡ θ

Então...

2 sin ⁡ θ ≤ r ≤ 2

Resumindo, a parte D 1 , pode ser descrita como:

π 4 ≤ θ ≤ π

2 sin ⁡ θ ≤ r ≤ 2

Passo 6

Para descrever a região D 2 , bem veja que o ângulo θ , está saindo de 180 ° e indo até a reta verde...

180 ° ≤ θ ≤ r e t a   V e r d e

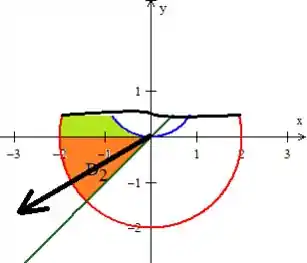
A reta verde, como vimos, tem ângulo de 45 ° com relação ao eixo x ...

180 ° ≤ θ ≤ 180 ° + 45 °

180 ° ≤ θ ≤ 225 °         o u                 π ≤ θ ≤ 5 π 4

Já o raio, bem... Esse varia da origem até o raio da vermelha nessa segunda parte...

0 ≤ r ≤ 2

Resumindo, a parte de D 2 , se escreve...

  π ≤ θ ≤ 5 π 4

0 ≤ r ≤ 2

Passo 7

Agora é só montar a integral basicamente...

Á r e a   d e   D = ∬ D   1   d A

Lembrando-se que separamos a região D em outras duas...

Á r e a   d e   D = ∬ D 1   1   d A + ∬ D 2   1   d A

Sendo D 1 ...

π 4 ≤ θ ≤ π

2 sin ⁡ θ ≤ r ≤ 2

E D 2 ...

  π ≤ θ ≤ 5 π 4

0 ≤ r ≤ 2

Temos...

Á r e a   d e   D = ∫ π 4 π ∫ 2 sin ⁡ θ 2 1 ⋅ J   d r d θ + ∫ π 5 π 4 ∫ 0 2 1 ⋅ J   d r d θ

Veja que não se pode esquecer do Jacobiano como eu disse . Assim, a área de região D fica...

Á r e a   d e   D = ∫ π 4 π ∫ 2 sin ⁡ θ 2 r   d r d θ + ∫ π 5 π 4 ∫ 0 2 r   d r d θ

Resposta

∫ π 4 π ∫ 2 sin ⁡ θ 2 r   d r d θ + ∫ π 5 π 4 ∫ 0 2 r   d r d θ

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}