Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 116123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1: Sejam 0 < a < b < 1 dois números reais positivos. Calcule a integral dupla ∬ Ω   1 x   d A , onde

Ω = x ,   y |   a x ≤ y ≤ b x ,   2 x ≤ x 2 + y 2 ≤ 4 x .

Passo 1

Vamos começar desenhando a nossa região!

x 2 + y 2 = 2 x

É uma circunferência de raio 1 e deslocada uma unidade em x , pois lembrando que x - 1 2 = x 2 - 2 x + 1 :

x 2 - 2 x + y 2 = 0           →

x - 1 2 - 1 + y 2 = 0         →

x - 1 2 + y 2 = 1

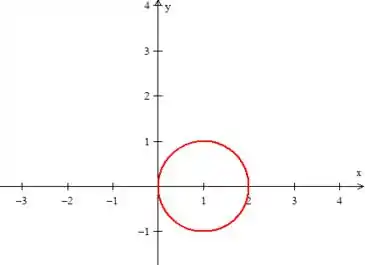
Viu só?! Semelhantemente x 2 + y 2 = 4 x é uma circunferência de raio 2 e deslocada duas unidades em x , assim:

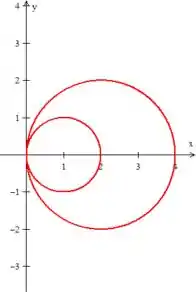
Além disso, sabemos que a região deve estar acima da reta y = a x e abaixo da reta y = b x :

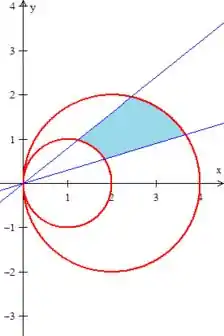
Entendeu?

Passo 2

ORA! Se estivermos trabalhando com uma região circular nada mais justo que pensarmos nas coordenadas polares:

x = r cos ⁡ θ

y = r sin ⁡ θ

x 2 + y 2 = r 2

J = r

Agora temos que descobrir quais são os limites de integração de r e θ , vamos nessa?

Passo 3

Para isso, vamos comparar a região R com as verdadeiras variações de r e θ das coordenadas polares:

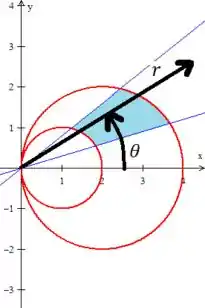
Veja que r varia de uma circunferência até a outra:

c i r c u n f e r ê n c i a   d e   r a i o   m e n o r ≤ r ≤ c i r c u n f e r ê n c i a   d e   r a i o   m a i o r

R e t a   m a i s   a b a i x o ≤ θ ≤ R e t a   m a i s   a c i m a

Vamos começar com a variação de r :

c i r c u n f e r ê n c i a   d e   r a i o   m e n o r :

x 2 + y 2 = 2 x     →         r 2 = 2 r cos ⁡ θ       →

r = 2 cos ⁡ θ

Enquanto isso:

c i r c u n f e r ê n c i a   d e   r a i o   m a i o r :

x 2 + y 2 = 4 x     →         r 2 = 4 r cos ⁡ θ       →

r = 4 cos ⁡ θ

Assim:

2 cos ⁡ θ ≤ r ≤ 4 cos ⁡ θ

Vamos ver os limites de θ agora:

R e t a   m a i s   a b a i x o :

y = a x     →         r sin ⁡ θ = a   r cos ⁡ θ       →

sin ⁡ θ cos ⁡ θ = a           →           tan ⁡ θ = a       →

θ = arctan ⁡ a

Enquanto isso:

R e t a   m a i s   a c i m a :

y = b x     →         r sin ⁡ θ = b   r cos ⁡ θ       →

sin ⁡ θ cos ⁡ θ = b           →           tan ⁡ θ = b       →

θ = arctan ⁡ b

Então:

arctan ⁡ a ≤ θ ≤ arctan ⁡ b

Passo 4

Finalmente podemos retornar à integral dupla:

∬ Ω   1 x   d A

E substituir as coordenadas polares, não se esquecendo do Jacobiano:

∬ Ω   1 x   d A = ∫ arctan ⁡ a arctan ⁡ b ∫ 2 cos ⁡ θ 4 cos ⁡ θ 1 r cos ⁡ θ ⋅ J   d r d θ =

∫ arctan ⁡ a arctan ⁡ b ∫ 2 cos ⁡ θ 4 cos ⁡ θ 1 r cos ⁡ θ ⋅ r   d r d θ = ∫ arctan ⁡ a arctan ⁡ b ∫ 2 cos ⁡ θ 4 cos ⁡ θ 1 cos ⁡ θ   d r d θ

Integrando...

∫ arctan ⁡ a arctan ⁡ b 1 cos ⁡ θ ∫ 2 cos ⁡ θ 4 cos ⁡ θ   d r d θ = ∫ arctan ⁡ a arctan ⁡ b 1 cos ⁡ θ 4 cos ⁡ θ - 2 cos ⁡ θ d θ =

∫ arctan ⁡ a arctan ⁡ b 1 cos ⁡ θ 2 cos ⁡ θ d θ = ∫ arctan ⁡ a arctan ⁡ b 2 d θ =

2 arctan ⁡ b - arctan ⁡ a

Resposta

2 arctan ⁡ b - arctan ⁡ a

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}