Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria

Exercício 112 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

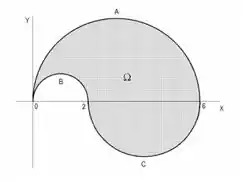
Seja o domínio representado na figura, onde é a parte da circunferência , é a parte da circunferência , é a parte da circunferência . Reescrever a integral dupla

na forma iterada:

3. usando coordenadas polares.

Passo 1

Para escrever em coordenadas polares, vamos primeiro dividir em duas regiões. Acima e abaixo do eixo x. Para descrever a parte de cima, fazemos a seguinte substituição:

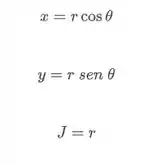
Aplicando essas substituições nas funções das circunferências:

Fazendo a substituição também em B:

Temos então que o raio varia da circunferência menor até a maior, logo

Já para a variação do , ele só dá de volta, o que seria . Então:

Escrevendo então a integral, substituindo os valores de x e y na integral e sem esquecer de adicionar o jacobiano no seu devido lugar.

Passo 2

Para descrever a parte abaixo do eixo x, vamos fazer com coordenadas polares centradas em (4,0), que é o centro da circunferência abaixo do eixo x.

Bom, pela imagem podemos ver que o raio varia entre 0 e 2 e o vai variar de até , ou seja, somente a metade debaixo da esfera de raio 2.

Passo 3

Juntando então as integrais temos:

Resposta

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .

Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]

Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y

Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .

Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}