Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 109123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Coordenadas polares

Seja

I = ∫ - 1 1 ∫ 1 1 + 1 - x 2 f x , y d y d x

  1. Inverta a ordem de integração em I .
  2. Calcule I para f x , y = 1 x 2 + y 2 .

Passo 1

a )

A região que ele descreve ali é do tipo I, temos - 1 ≤ x ≤ 1 e 1 ≤ y ≤ 1 + 1 - x 2

Antes de trocar essa ordem de integração, vamos fazer um esboço desse domínio.

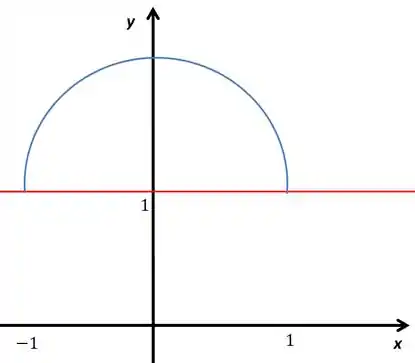
Passo 2

Para inverter a ordem de integração devemos saber o intervalo de y e depois descobrir as funções que x varia.

Repara que temos uma circunferência de raio 1 ali centrada no ponto 0,1

Isso nos diz que

1 ≤ y ≤ 2

A equação da circunferência vai ser

y = 1 + 1 - x 2

y - 1 2 = 1 - x 2

x 2 + y - 1 2 = 1

Repara que o valor de x vai da parte da esquerda da circunferência até a parte da direita. Se isolarmos x nessa equação da circunferência vamos ter

x 2 = 1 - y - 1 2

x = ± 1 - y - 1 2

O termo negativo é a parte da esquerda da circunferência, enquanto a parte positiva é a parte da direita da circunferência, então

- 1 - y - 1 2 ≤ x ≤ 1 - y - 1 2

Passo 3

A integral vai ficar

I = ∫ 1 2 ∫ - 1 - y - 1 2 1 - y - 1 2 f x , y d x d y

Passo 4

b )

Como tanto a função que vamos integrar como a região de integração possuem termos x 2 e y 2 , vamos utilizar coordenadas polares. Faremos, então:

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

Passo 5

Agora que já definimos a substituição que faremos, vamos analisar os novos intervalos de integração.

Repara que o ângulo θ vai variar de um extremo da circunferência até o outro. Olha o desenho com o ângulo marcado

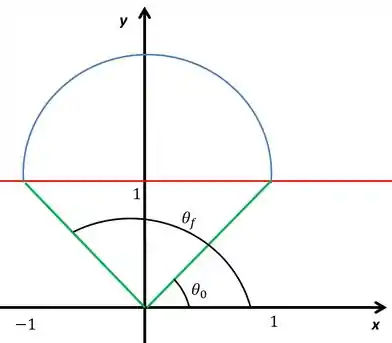
Ângulo θ 0 vai ser π 4 , isso porque temos um triângulo isósceles. Além disso, aquele ângulo do verde vai ser π 2 . Então

θ f = π 2 + π 4 = 3 π 4

O raio vai variar da curva vermelha para a curva azul, mas quanto será isso? Repara que temos dentro da circunferência a seguinte desigualdade

1 ≤ y ≤ 1 + 1 - x 2

Fazendo a substituição temos

1 ≤ r sen ⁡ θ ≤ 1 + 1 - r cos ⁡ θ 2

Da primeira desigualdade

r ≤ 1 sen ⁡ θ

Vamos para a segunda

r sen ⁡ θ ≤ 1 + 1 - r cos ⁡ θ 2

r sen ⁡ θ - 1 ≤ 1 - r cos ⁡ θ 2

r sen ⁡ θ - 1 2 ≤ 1 - r cos ⁡ θ 2

r 2 sen 2 ⁡ θ - 2 r sen ⁡ θ + 1 - 1 + r 2 cos 2 ⁡ θ ≤ 0

r 2 sen 2 ⁡ θ + cos 2 ⁡ θ - 2 r sen ⁡ θ ≤ 0

r 2 - 2 r sen ⁡ θ ≤ 0

r r - 2 sen ⁡ θ ≤ 0

Como r ≥ 0 sempre, teremos:

r - 2 sen ⁡ θ ≤ 0   → r ≤ 2 sen ⁡ θ  

D = { ( r , θ ) | 1 sen ⁡ θ ≤ r ≤ 2 sen ⁡ θ ;   π / 4 ≤ θ ≤ 3 π / 4 }

Passo 6

Vamos montar a integral com as coordenadas polares

I = ∫ 1 2 ∫ - 1 - y - 1 2 1 - y - 1 2 1 x 2 + y 2 d x d y

I = ∫ π / 4 3 π / 4 ∫ 1 sen ⁡ θ 2 sen ⁡ θ r r cos ⁡ θ 2 + r sen ⁡ θ 2 d r d θ

⇒ ∫ π / 4 3 π / 4 ∫ 1 sen ⁡ θ 2 sen ⁡ θ r r 2 d r d θ

⇒ ∫ π / 4 3 π / 4 ∫ 1 sen ⁡ θ 2 sen ⁡ θ 1 d r d θ

⇒ ∫ π / 4 3 π / 4 2 sen ⁡ θ - 1 sen ⁡ θ d θ = ∫ π / 4 3 π / 4 2 sen ⁡ θ - cossec ⁡ θ d θ

⇒ - 2 cos ⁡ θ - - ln ⁡ cossec ⁡ θ + cot ⁡ θ θ = π / 4 3 π / 4 = - 2 cos ⁡ θ + ln ⁡ cossec ⁡ θ + cot ⁡ θ θ = π / 4 3 π / 4

⇒ - 2 cos ⁡ 3 π 4 + ln ⁡ cossec ⁡ 3 π 4 + cot ⁡ 3 π 4 - - 2 cos ⁡ π 4 + ln ⁡ cossec ⁡ π 4 + cot ⁡ π 4

⇒ 2 2 2 + ln ⁡ 2 - 1 - - 2 2 2 + ln ⁡ 2 + 1

⇒ 2 2 2 + ln ⁡ 2 - 1 + 2 2 2 - ln ⁡ 2 + 1

⇒ 2 2 + ln ⁡ 2 - 1 - ln ⁡ 2 + 1

⇒ 2 2 + ln ⁡ 2 - 1 2 + 1

Resposta

I = ∫ 1 2 ∫ - 1 - y - 1 2 1 - y - 1 2 f x , y d x d y

2 2 + ln ⁡ 2 - 1 2 + 1

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}