Utilize as coordenadas polares para determinar o volume do sólido dado.
b) Dentro da esfera e a fora do cilindro
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume do sólido que tá dentro da esfera (em vermelho) e a fora do cilindro (em azul):
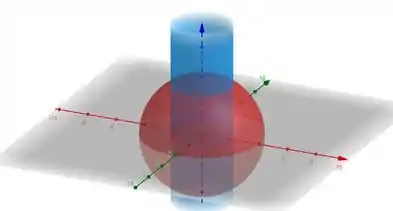
Mas que bom que existe uma fórmula pra calcular esse volume, que é dada pela integral:
Onde é a nossa região de integração. Repare que, como a gente tem essa geometria circular, fica mais fácil calcular nossa integral usando as coordenas polares, que são convertidas de acordo com as equações:
Assim, a gente percebe que nossa região tem um ângulo de variação , no intervalo . E o nosso raio varia da borda do cilindro, , até a borda da esfera, , ou seja, . Então, vamos fazer essas substituições na nossa integral.
Vamos lá!
Passo 2
Nossa integral é dada por:
Usando a equção da esfera, com e substituindo as equações de transformação que vimos no passo , temos:
Além disso, nós temos os intervalos de integração e . Substituindo tudo na integral:
Passo 3
Pra calcular essa integral, vamos fazer:
Assim, temos:
Integrando primeiro em relação a :
Aplicando os intervalos de integração em :
Agora integrando em relação a :
E aplicando os limites de integração em :
Valeu, galera! Até a próxima! 😉