UFPE – Cálculo 1 – Listas de C1 - MQCC1 – 2ª Lista – 2023.1 – Exercício 4a
Uma certa locadora de automóveis cobra R$ 35,00 por dia mais 55 centavos por quilômetro rodado.
(a) Expresse o custo para alugar um carro nessa locadora por 1 dia em função do número de quilômetros rodados e desenhe o gráfico relacionado.
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Bom, para montarmos a equação do custo da nossa locadora, precisamos analisar o enunciado e ver qual vai ser o custo fixo e qual vai ser o custo variável.
Para isso, vamos usar a fórmula geral da equação de 1º Grau:
Show, e com isso vamos atrás de cada componente.
Passo 2
Vamos lá.
O nosso exercício se trata de montar uma equação do 1º grau que expresse o custo total em função do número de unidades produzidas.
O enunciado diz que existe um custo fixo de R$ 35,00 por dia, independente da quantidade de quilômetros rodados. Ou seja, esse valor é referente ao coeficiente linear (b).
Além disso, há um custo de R$ 0,55 por quilômetro rodado. Aqui é um custo dependente da variável. Assumindo que a nossa variável vai ser cada quilômetro rodado (x), podemos dizer que esses R$ 0,55 são referentes ao coeficiente angular, logo:
Logo:
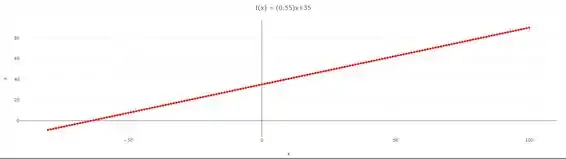
Passo 3
Pegando as informações do Passo anterior, vamos traçar o gráfico:
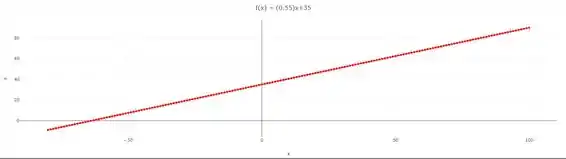
Resposta
