Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Otimização

Ver Teoria
Exercício 113123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 7.36

Considere todos os triângulos retângulos formados pelos semieixos positivos e por uma reta que passa pelo ponto ( 1,2 ) . Dentre todos esses triângulos, aquele que possui área mínima tem a hipotenusa valendo:

a )   18

b )   20

c )   38

d )   24

e )   40

Passo 1

Fala galera, tudo bem com vocês?

Nessa questão temos mais um problema de otimização.

Temos triângulos retângulos que são formados nos semieixos x e y positivos, e a hipotenusa encontra-se na reta que passa pelo ponto ( 1,2 ) .

Sobre essa categoria de triângulos queremos encontrar a hipotenusa daquele que possui área mínima.

Então pessoal, como temos um triângulo retângulo onde x e y são os catetos, área dele será dada por:

A   = x y 2

Precisamos conseguir relacionar x e y através da informação de que a hipotenusa passa pelo ponto ( 1,2 ) . A ideia aqui é utilizarmos semelhança de triângulos!

Vem comigo que vai ficar bem claro 😊

Passo 2

Segundo o que foi falado no enunciado, podemos montar a seguinte geometria:

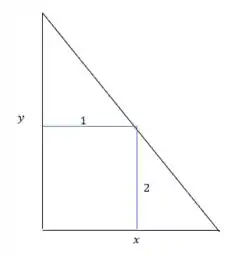
Daí, pela semelhança de triângulos podemos escrever:

y - 2 1 = 2 x - 1

Logo:

y = 2 x - 1 + 2

Perfeito!

Daí, voltando para a área do triângulo, temos:

A = 1 2 ⋅ 2 x - 1 + 2 ⋅ x

= 1 2 ⋅ 2 x x - 1 + 2 x

Então, agora que conseguimos uma expressão para a área em função apenas de A , podemos derivá-la e igualar a 0 para encontrar os pontos críticos.

Passo 3

Fazendo d A / d x , temos:

d A d x = 1 2 ⋅ 2 x x - 1 + 2 x ' = 0

Como a derivada da soma é a soma das derivadas, temos:

d A d x = 1 2 ⋅ 2 x x - 1 ' + ( 2 x ) '

Resolvendo a derivada de cada um desses termos, e começando pelo primeiro usando a regra do quociente, temos:

2 x x - 1 ' = 2 ⋅ x - 1 - 2 x x - 1 2

=   - 2 x - 1 2

Massa! Já para o segundo termo, vamos ter:

2 x ' =   2

Substituindo de volta em d A d x , temos:

d A d x = 1 2 ⋅ - 2 x - 1 2 + 2 = 0

Logo:

- 2 x - 1 2 + 2 = 0

∴ 2 x - 1 2 = 2

Logo:

x - 1 2 = 1

x 2 - 2 x + 1 = 1

⇒ x 2 - 2 x = 0

x 2 = 2 x

Nota que a solução x = 0 não nos interessa né? Porque aí não teríamos triângulo retângulo nenhum na jogada.

Logo:

x = 2

Como só temos um ponto crítico, e a questão pede a área mínima, não precisamos nem perder tempo verificando se esse é um ponto de máximo ou mínimo.

Pra calcular a hipotenusa, basta fazermos:

x 2 + y 2

Como:

y = 2 x - 1 + 2

Temos:

y = 2 2 - 1 + 2

= 4

Logo:

x 2 + y 2 = 2 2 + 4 2

= 20

Prontinho, temos a letra b ) .

E aí, curtiram a solução? Responde Aí!

Resposta

b

Exercícios de Livros Relacionados

Encontre a área do maior retângulo que pode ser inscrito na elipse x 2 a 2 + y 2 b 2 = 1
Um modelo usado para a produção Y de uma colheita agrícola como função do nível de nitrogênio N no solo (medido em unidades apropriadas) é Y = k N 1 + N 2 Em que k é um constante positiva. Que nível d
Gerentes de lojas querem uma política de estoque ótima. Excesso de estoque resulta em armazenagem excessiva e custos de estoque, enquanto que um estoque pequeno significa adicionar custo à reorganizaç
Um cilindro circular reto é inscrito em uma esfera de raio r . Encontre o maior volume possível para este cilindro.
Um cilindro circular reto é inscrito em um cone com altura h e raio da base r . Encontre o maior volume possível para este cilindro.