Dado o triângulo retângulo de catetos e , determine o retângulo de maior área que está inscrito no triângulo de modo que um dos lados está contido na hipotenusa.
Passo 1
Eaee!!! Belezinha? Bom... Para resolver essa questão, primeiramente temos que desenhar o triângulo retângulo, com um retângulo dentro dele:
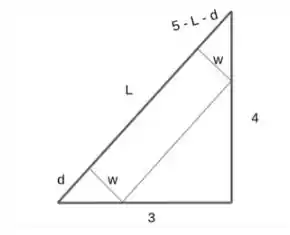
Agora que entendemos nossa figura, vamos encontrar a área do nosso retângulo!!
Quer saber como? Então bora junto!!
😉
Passo 2
Assim, das relações de proporcionalidade dos triângulos retângulos, temos para o triângulo inferior:
E, para o triângulo superior:
Dessa forma, temos:
Assim, como temos os tamanhos da base e do lado do retângulo, podemos encontrar sua área :
Passo 3
Agora, para encontrarmos o maior valor possível de área, vamos derivar a expressão que acabamos de descobrir e igualar a zero:
E o valor de , ao substituir , é:
Entendeu direitinho? Responde aee ;)

Resposta
Retângulo de lados e .