Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Otimização

Ver Teoria
Exercício 112123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 7.33

Dentre os cilindros circulares inscritos numa esfera de raio 1 , seja h 1 a altura daquele que tem volume máximo e seja h 2 a altura daquele que tem superfície lateral máxima. Então, h 1 / h 2 é:

a ) 2 5

b ) 3 5

c ) 2 3

d )   2

e )   3

Passo 1

Fala aí pessoal, tudo tranquilo com vocês?

Nessa questão temos um cilindro circular reto que se encontra inscrito em uma esfera de raio 1 . Queremos calcular a altura h que:

- Maximiza o volume do cilindro (vamos chamar essa altura de h 1 );

- Maximiza a área da superfície lateral do cilindro (vamos chamar essa altura de h 2 ) ;

Vocês lembram como calculamos o volume e a área lateral de um cilindro? Vamo revisar...

V = π d 2 4 h 1

A L = π d h 2

onde d é o diâmetro da base do cilindro. Beleza?

Massa! Então, a ideia geral desse exercício é usarmos o fato de o cilindro estar inscrito na esfera pra encontrar uma relação entre d e h ; e, a partir daí, substituir em V e em A L para derivar as expressões resultantes e igualá-las a zero.

Vem comigo que vai ficar bem claro 😊

Passo 2

Pra começar vamos encontrar a relação entre d e h .

Como o cilindro está inscrito na circunferência, podemos tomar a seguinte secção transversal:

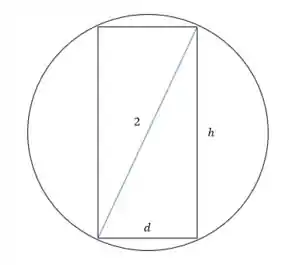
A reta em azul vale 2 pois representa duas vezes o raio da esfera.

Dessa geometria, pelo teorema de Pitágoras no triângulo retângulo formado, temos:

2 2 = d 2 + h 2

∴ 4 = d 2 + h 2

Logo:

d 2 = h 2 - 4

d = h 2 - 4

Perfeito!

Passo 3

Vamos então começar calculando a altura h 1 que maximiza o volume do cilindro. Temos que:

V = π d 2 4 ⋅ h 1

Substituindo:

d 2 = h 2 - 4

Vem:

V = π h 1 2 - 4 h 1 4

Derivando e igualando a zero, vem que:

d V d h 1 = 3 π h 1 2 4 - π = 0

⇒ 3 π h 1 2 4 = π

Logo:

h 1 2 = 4 3

⇒ h 1 = 2 3 3

Muito bom!

Passo 4

Vamos agora calcular a altura h 2 que maximiza a área lateral da circunferência:

A L = π d h 2

Como:

d = h 2 - 4

Temos:

A L = π h 2 2 - 4 1 2 h 2

Vamos derivar essa expressão e igualar a zero!

d A L d h 2 = π h 2 2 - 4 1 2 + π h 2 ⋅ 1 2 ⋅ 2 h 2 h 2 2 - 4 1 2 = 0

∴ h 2 2 - 4 + h 2 2 h 2 2 - 4 1 2 = 0

Logo:

2 h 2 2 - 4 = 0

∴ h 2 = 2

Daí, fazendo:

h 1 h 2

Temos:

h 1 h 2 = 2 3 3 2 = 2 3 ⋅ 3 2

= 2 3

Ou seja, letra c ) de casa!

Valeeeeu gente, até a próxima 😊

Resposta

c )  

Exercícios de Livros Relacionados

Encontre a área do maior retângulo que pode ser inscrito na elipse x 2 a 2 + y 2 b 2 = 1
Um modelo usado para a produção Y de uma colheita agrícola como função do nível de nitrogênio N no solo (medido em unidades apropriadas) é Y = k N 1 + N 2 Em que k é um constante positiva. Que nível d
Gerentes de lojas querem uma política de estoque ótima. Excesso de estoque resulta em armazenagem excessiva e custos de estoque, enquanto que um estoque pequeno significa adicionar custo à reorganizaç
Um cilindro circular reto é inscrito em uma esfera de raio r . Encontre o maior volume possível para este cilindro.
Um cilindro circular reto é inscrito em um cone com altura h e raio da base r . Encontre o maior volume possível para este cilindro.