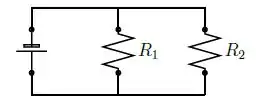
Quando dois resistores e são ligados em paralelo (veja a figura), a resistência total é dada pela equação . Se e estão aumentando as taxas de e respectivamente, a que taxa varia no instante em que e ?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa de variação de no instante em que e , então a gente quer encontrar um .
Pra isso, ele nos disse que e estão aumentando as taxas de e , respectivamente. Isso quer dizer que:
E
Além disso, eles nos deu a equação da resistência total nessa configuração em paralelo, que é:
Então, o que nós vamos fazer, pra fazer aparecer o ali, é derivar essa equação implicitamente em relação a e substituir os dados do enunciado.
Vamos lá!
Passo 2
Derivando a expressão da resistência, temos:
Passo 3
A gente já sabe que , , e . Mas falta o . E pra descobrir o valor dele, vamos usar a equação que o enunciado nos deu:
Substituindo os valores de e :
Passo 4
Agora temos tudo que precisamos para voltar a nossa equação do passo e substituir:
Portanto, a taxa de variação , no instante em que e , é .
Valeu, galera! Até a próxima! 😉