USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 7.38
Um muro de metros de altura está a metro de distância da parede lateral de um prédio. Qual o comprimento da menor escada cujas extremidades se apoiam uma na parede, e outra no chão do lado de fora do muro?
Passo 1
Fala aí gente, tudo bem com vocês?
Nessa questão temos mais um probleminha de otimização.
Basicamente, temos um muro de metros que está do lado exterior de uma parede lateral de um prédio. Queremos, a partir do solo do lado exterior ao muro, colocar uma escada que alcance a parede do prédio.
Essa escada não precisa alcançar o topo da parede do prédio, ela precisa apenas se apoiar nela. E, para isso, fica subentendido que precisamos considerar a parede grande o suficiente, beleza?
Basicamente, a situação descrita se encaixa nessa imagem:
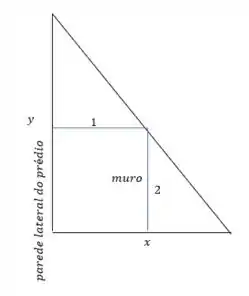
Sacaram a ideia? A escada é justamente a hipotenusa desse triângulo.
Vamos então usar o teorema de Pitágoras para calcular a hipotenusa, e depois buscamos relacionar e para usar a otimização na expressão da hipotenusa. Ou seja, derivar e igualar a zero.
Vamo nessa!
Passo 2
Pelo teorema de Pitágoras, podemos dizer que:
onde é o comprimento da hipotenusa.
Pela semelhança de triângulos, temos:
Logo:
Substituindo na expressão da hipotenusa, temos:
Perfeito! Então encontramos uma expressão da hipotenusa apenas função de . Aí é derivar, igualar a zero, e correr pro abraço 😊
Passo 3
Fazendo , vem que:
Pela regra da cadeia:
Pra essa expressão ser nula, precisamos que:
Então:
Logo:
Como a solução não nos interessa (pois o tamanho da parede teria que ser infinito, o que é impossível), temos que:
Tirando a raiz cúbica:
Daí, temos que:
Logo:
Assim:
E é isso gente!
Muito obrigado pela atenção de vocês 😊