Sejam . Determine, caso exista, o perímetro mínimo dos triângulos de base e altura (relativa à base dada) .
Passo 1
Fala aí pessoal, tudo bem com vocês?
Nessa questão, temos um triângulo cujo um dos lados vale e a altura relativo à esse lado vale . Precisamos determinar qual o perímetro mínimo desse triângulo.
Então gente, o perímetro é dado pela soma dos lados do triângulo. O problema é que temos apenas um dos lados do triângulo em questão, ou seja, precisamos relacionar e para encontrar os outros dois lados.
Para fazer isso vamos dividir o nosso lado em dois pedaços, segundo a altura . A partir daí, usamos o teorema de Pitágoras pra relacionar o lado do triângulo com e com um dos pedaços de .
Não pegou a ideia? Vem comigo que vai ficar bem explicadinho... 😊
Passo 2
Então, vamos desenhar o que o enunciado nos deu. Mas, vamos dividir também o lado do triângulo em duas partes: e . Divisão feita segundo a altura .
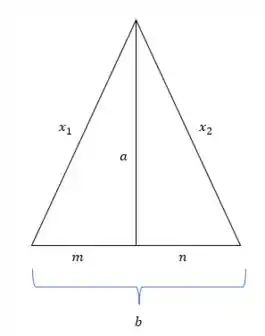
O perímetro desse triângulo será dado por:
Como é uma constante, basicamente queremos minimizar a soma de e . Mas, da desigualdade das médias, temos que:
Ou seja:
Assim:
Logo, teremos o valor mínimo da soma justamente quando ocorrer a igualdade:
Elevando ao quadrado essa equação, temos:
Logo:
Ou seja:
Isso significa que a soma será mínima quando ocorrer a igualdade:
Assim, como teremos um triângulo isósceles, para o e que vimos na figura anterior, vale que:
Mas, pelo teorema de Pitágoras podemos escrever que:
E, como o triângulo é isósceles:
Passo 3
Podemos então calcular o perímetro do triângulo como sendo:
Logo:
É isso gente, matamos a questão!
Trouxemos uma ideia um pouco diferente, usando a desigualdade das médias.
Espero que vocês tenham curtido!