USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 7.34
Sejam e duas retas paralelas com a distância entre eles igual a . Fixe um ponto sobre a reta . Fixe dois pontos e sobre a reta de modo que a distância entre os pontos e seja igual a . É possível encontrar um ponto na reta , de modo que o segmento intercepte o segmento em um ponto de forma que a soma das áreas dos triângulos e seja mínima? E seja máxima? Nos casos em que a resposta for afirmativa, determine a altura do triângulo
Passo 1
Fala aí galera, tudo beleza?
Nessa questão temos mais um probleminha de otimização.
Basicamente, temos dois triângulos opostos pelo vértice , cujos lados estão nas retas e . Na reta temos o lado de tamanho . Na reta , temos o lado . Não sabemos o tamanho desse segundo lado, mas sabemos que a distância entre e vale .
Massa!
Sabendo de tuudooo isso precisamos calcular as somas mínima e máxima das áreas dos triângulos, se elas existire.
Pra fazer isso, precisamos escrever uma expressão para a soma em um caso genérico, derivá-la e igualar a zero. Assim, devemos ter duas soluções para a altura que corresponde a essas somas!
Vem comigo que tudo isso vai ficar bem mais claro 😊
Passo 2
Bom, pra começar vamos fazer um esboço da situação descrita no enunciado:
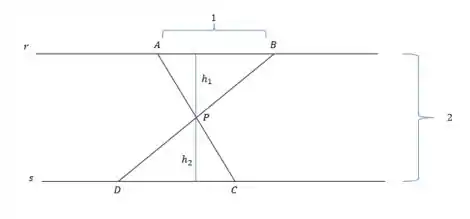
A partir dessa figura podemos escrever a área dos triângulos e .
E:
Mas precisamos conseguir escrever em função dos outros valores que temos. Por isso, vamos usar a semelhança dos triângulos e (caso . Temos:
Logo:
Substituindo na expressão da área, vem que:
Excelente! Vamos então escreve a soma da área desses triângulos como:
Mas, ainda pela figura também sabemos que:
Portanto:
Assim:
Muito bom gente!
Passo 3
Agora que já temos uma expressão para a área dos triângulos, podemos derivar em relação a e igualar a zero.
Temos:
Usando que a derivada da soma é a soma das derivadas:
Vamos fazer essas derivadas termo a termo:
O próximo termo é um pouco mais complicado, e precisamos usar a regra do quociente:
Daí, vamos ter:
Excelente! Voltando para a nossa equação principal, temos:
Vamos resolver essa equação:
Assim:
Logo:
Ou seja, só temos um ponto crítico, que pode ser de máximo ou mínimo. Mas, analisando bem a nossa expressão para :
Vemos que quando , a nossa expressão tende a infinito. Ou seja, não conseguimos determinar uma área máxima. Logo:
é ponto de mínimo.
É isso gente, espero que vocês tenham curtido!
Até a próxima 😉
Resposta
ponto de mínimo