Um tanque tem a forma de um cone circular reto invertido, com metros altura e metros de raio da base. Se a água entra no tanque à razão de , calcule aproximadamente a razão na qual o nível da àgua subindo quando a profundidade é de metro.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a razão na qual o nível da àgua está subindo quando a profundidade é de metro. Então, vamos considerar que o volume de água nesse tanque cônico de altura e raio é dado por:
Que é a fórmula do volume do cone. Nesse caso, temos a informação de que e queremos descobrir quando . Olha só nosso sistema:
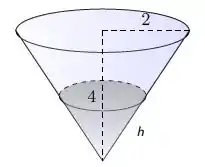
A altura do nível de água, o raio da lâmina de água da superfície e o volume de água dependem do tempo . E nós devemos descrever esse volume em função apenas da altura. Então, vamos usar a semelhança de triângulos, de acordo com a figura acima, para obter uma relação entre raio e altura. Daí vamos substituir essa relação na equação do volume do cone, derivar a equação implicitamente e aplicar os dados numéricos para descobrir nosso resultado.
Vamos lá!
Passo 2
Por semelhança de triângulo, na figura do passo , temos:
Isolando :
Passo 3
Substituindo na equação do volume, temos:
Derivando essa expressão implicitamente, vamos ter:
Olhá só, apareceu o nosso termo de interesse . Então, substituindo e , temos:
Simplificando:
Logo, a altura do nível de água está subindo a uma taxa de .
Valeu, galera! Até a próxima! 😉