Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Base

Ver Teoria
Exercício 28123456789101112131415161718192021222324252627293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

USP; Sem campus; Álgebra Linear 1; P1; 2022; Questão 15

Seja E uma base de V 3 . Assinale a alternativa correspondente ao vetor v   ∈   V que torna o conjunto

{ v , ( 1 ,   − 1 ,   1 ) e   , ( 2 ,   1 ,   3 ) e   }

linearmente independente.

  1. v   =   ( 3 ,   1 ,   4 )
  2. v   =   ( − 1 , �� 4 ,   0 )
  3. v   =   ( − 1 ,   4 ,   0 )
  4. v   =   ( − 1 ,   7 ,   1 )
  5. v   =   ( 2 ,   − 2 ,   2 )

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Essa é bem bacana, pois vmos visitar uma condição para um conjunto de vetores serem LI.

Bem, Queremos que o conjunto de vetores

{ v , ( 1 ,   − 1 ,   1 ) e   , ( 2 ,   1 ,   3 ) e   }

Seja LI. Como podemos verificar isso? Ora, um possível teste é ver se a matriz cujas colunas são os vetores deste conjunto tem determinante diferente de zero. Ou seja, se v = ( a , b , c ) , queremos ver quais as condições necessárias para que

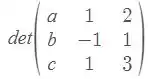
Seja diferente de zero.

Passo 2

Vamos calcular

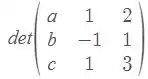
Usando a regra para o determinante 3 x 3 , obtemos

= ( - 3 a + c + 2 b ) - ( 3 b + a - 2 c )

= - 3 a + c + 2 b - 3 b - a + 2 c

= - 4 a + 3 c - b

Agora que temos essa condição, basta verificarmos quais vetores das alternativas satisfazem que

- 4 a + 3 c - b ≠ 0

Checando, podemos observar que o vetor v   =   ( 3 ,   1 ,   4 ) , é tal que

- 4 * 3 - 1 + 3 * 4 = - 1

Logo esse vetor satisfaz a condição para o determinante ser diferente de zero. Então o conjunto

{ v , ( 1 ,   − 1 ,   1 ) e   , ( 2 ,   1 ,   3 ) e   }

é LI para v   =   ( 3 ,   1 ,   4 )

Vetor presente na alternativa a )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

a )

Exercícios de Livros Relacionados

Demonstrar que é L.I o conjunto { 1 ,x - a ,x - a 2 ,… ,x - a n - 1 } De vetores de P n - 1 ( R ) , onde a é um número arbitrário.
Quais dos conjuntos de vetores dados são bases de P 2 ?c) 1 +x +x 2 ,x +x 2 ,x 2
Quais dos conjuntos de vetores dados são bases de P 2 ?a) 1 -3 x +2 x 2 ,1 +x +4 x 2 ,1 -7 x
Verificar quais dos seguintes conjuntos de vetores formam base do R 2 . { 1 ,2 ,- 1 ,3 } { 3 ,- 6 ,- 4 ,8 } { 0 ,0 ,2 ,3 } { 3 ,- 1 ,2 ,3 }
Prove que vec u = 0 = vec u = (0 , 0 , 0)_E .