Seja B uma base ortonormal de e considere os vetores:
Seja o vetor paralelo a tal que seja ortogonal a . A norma do vetor 2 é igual a:
Passo 1
Falaaaa, blz??? Bora para mais uma questãozinha envolvendo achar norma de vetores. Nessa questão ocorre algo interessante, ele diz sobre vetores paralelos e a subtração de vetores sendo ortogonal, temos um conceito que engloba essas informações, consegue lembrar?
É o conceito de projeção, vamos desenhar para ver o que acontece aqui:
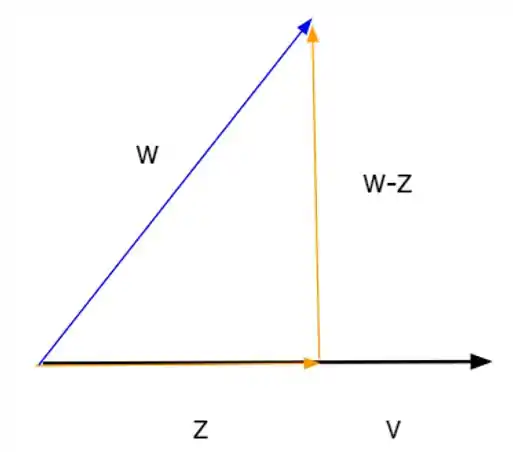
Ou seja, nesse problema, temos que por definição
Passo 2
Agora que sabemos isso, vamos aplicar a fórmula de projeção:
Usaremos que:
E
Aplicando na fórmula:
Passo 3
Agora temos o que precisamos para acabar a questão, bora lá:
E assim acaba mais um problema, uma questão que necessita que a gente tenha uma sacada para perceber essa questão da projeção, porém uma ideia que é comum de aparecer, bora para a próxima??
Resposta
Letra A