Suponha que são planos cuja interseção é a reta r. Sejam vetores não-nulos tais que e , e seja um vetor não-nulo paralelo a r. Considere as seguintes afirmações:
- Os vetores são paralelas;
- , é um base ortogonal de ;
- Os vetores são linearmente independentes.
Passo 1
Falaaaa, blz??? Vamos começar essa questãozinha desenhando um esboço para nos ajudar a entender o que está rolando
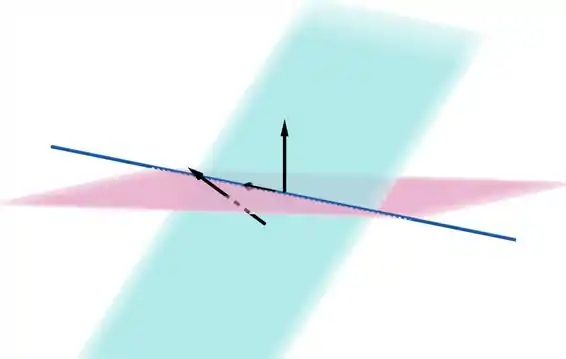
Nessa figura, vamos supor que é o plano horizontal (o plano roxo) e o vetor vertical é nosso .
O outro plano (azul) é o nosso e o vetor perpendicular a ele é nosso . O vetor que está na reta será nosso .
Passo 2
Vamos analisar a afirmação (I):
Primeiro vale ressaltar o que significa.
Quando fazemos o produto vetorial entre dois vetores isso nos resulta num terceiro vetor perpendicular aos outros 2.
Agora vamos olhar para a figura e notar o seguinte, nosso vetor paralelo a reta (é perpendicular aos vetores , logo quando fizermos o produto vetorial, que resultará num vetor perpendicular a ele será paralelo ao nosso . Então a primeira afirmação está correta.
Passo 3
Agora vamos analisar a segunda afirmação.
Bom, essa alternativa é bem direta que é falsa e olhando para nossa figura fica bem fácil enxergar isso.
Para que a base mencionada seja ortogonal, os nossos vetores da base deveriam ser perpendiculares dois a dois, porém nada indica que tenham que se perpendiculares.
Passo 4
Essa afirmação (III) é um pouco mais trabalhosa, porém não muito complexa. Vamos com calma para não gerar confusão.
Vamos lembrar que 3 vetores são linearmente independentes, quando não conseguimos escrever 1 como combinação dos outros 2, ou em termos matemáticos:
só ocorre quando
Então vamos lá. Para os 3 vetores citados serem L.I, temos que:
Queremos achar que
Vamos correr atrás disso, então:
Multiplicando (fazendo produto escalar) da equação por
Como ) e são perpendiculares a , temos que
Logo
Como
Uhuuul! Achamos ! Bora achar os outros...
Passo 5
Então como , ficamos com:
Fazendo a mesma ideia (multiplicar a equação), porém fazendo o produto escalar com :
Como é perpendicular a
Então ficamos com:
Nesse caso tiramos que , uma vez que o produto misto de 3 vetores é zero em 3 situações:
- um deles é nulo
- dois deles são colineares
- se os 3 são coplanares
e nenhuma delas é verdade aqui! Então
Passo 6
Por fim, nos resta que
Daqui tiramos que , pois um produto vetorial só é nulo quando algum dos vetores é nulo ou se os vetores não são L.I.
Como são L.I e diferentes do vetor nulo, então . Então, concluímos que
Logo , que era o que estávamos buscando :)
Resposta
Letra A