USP – Álgebra Linear – P1 2020 – Questão 4
Seja uma base ortonormal de . Considere, em , o triângulo de vértices , em que e . A altura desse triângulo relativa ao vértice é igual a
Passo 1
E aí gente, belezinha??
Olha só, temos um triângulo assim:
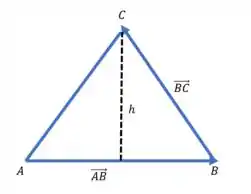
(isso é só uma forma de desenhar, se você tiver imaginado um triângulo diferente desse, não tem problema hahahaha)
O que importa aqui é que queremos encontrar a altura , que vem do vértice
Para isso, vamos lembrar que a área de um triângulo é metade da área do paralelogramo. E a área do paralelogramo é o módulo do produto vetorial de e . Então
Mas também sabemos que a área de um triângulo é , então também podemos escrever
Igualando as duas fórmulas, temos
Portanto:
Uhhhh sucesso! Então vamos lá usar isso!
Passo 2
Vamos começar encontrando . Sabendo que e , esse produto vetorial é dado pelo determinante dessa matriz:
Calculando o determinante:
Logo, o produto vetorial vai ser
E o seu módulo é
Passo 3
Legal, então temos
Onde
Então
Então:
Ufa! Deu bom hahahaha