UTFPR– Equações Diferenciais – Lista 3 – Questão 3b
Frequentemente, uma pequena mudança na condição inicial ou na equação diferencial, geram uma mudança radical na solução da equação diferencial. Nos problemas de (a) até (d), encontre uma solução explícita para o problema de valor inicial dado, trace um gráfico da solução encontrada e compare cada curva da solução em uma vizinhança de (0;1).
Passo 1
E aí, tudo bem? Essa questão é o começo de uma longa lista, e vou te ajudar em cada uma das questões! Começando por essa edo bonitinha
Vamos relembrar a técnica de resolução que já conhecemos:
- Variáveis separáveis: para aplicar esse método precisamos jogar tudo que envolve para um lado, tudo que envolve para o outro e integrar!
Como podemos separar de um lado tudo que tem , e para outro tudo que tem , então é esse o método certo! E depois? Bom, esse é um problema de valor inicial, então achada a solução, precisamos ainda aplicar a condição dada para achar a constante!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Já descobrimos qual o método que vamos usar, agora é #partiusolução
No método de variáveis separáveis, precisamos jogar tudo que tem para um lado e tudo que tem do outro e integrar!
Tudo bem até aqui?
Integrando temos
Passo 3
Agora por fim aplicar a condição inicial para achar aquele
Do passo anterior
Do enunciado temos , daí
Beleza?
Aí nossa solução fica assim:
Comparando com a solução
Temos
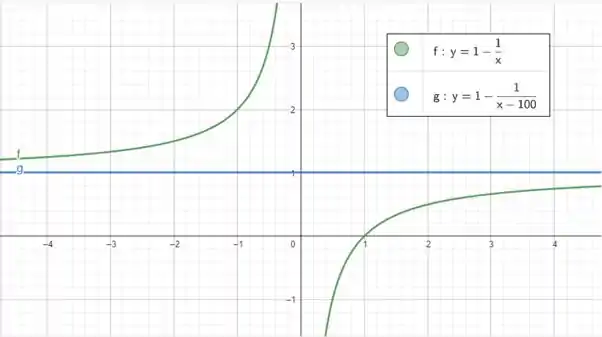
E é isso! Espero ter ajudado! Vamos para a próxima?