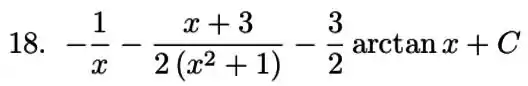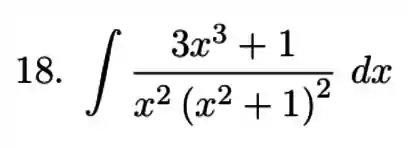
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Frações Parciais

Ver Teoria
Exercício 812345679101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Para começar precisamos decidir as frações parciais do nosso problema. Nesse caso, temos raízes múltiplas, então

3 x 3 + 1 x 2 x 2 + 1 2 = A x 2 + B x 2 + 1 + C x 2 + 1 2

Se manipularmos um pouquinho

3 x 3 + 1 x 2 x 2 + 1 2 = A x 2 + 1 2 x 2 x 2 + 1 2 + B x 2 ( x 2 + 1 ) x 2 x 2 + 1 2 + C x 2 x 2 x 2 + 1 2

3 x 3 + 1 = A x 4 + 2 x 2 + 1 + B x 4 + x 2 + C x 2

3 x 3 + 1 = A x 4 + 2 A x 2 + A + B x 4 + B x 2 + C x 2

3 x 3 + 1 = x 4 A + B + x 2 2 A + B + C + A

3 x x 2 + 1 = x 4 A + B + x 2 2 A + B + C + A

Logo

A = 1

A + B = 0

B = - 1

E

2 A + B + C = 3 x

C = 3 x - 1

Então ficamos com

3 x 3 + 1 x 2 x 2 + 1 2 = 1 x 2 - 1 x 2 + 1 + 3 x - 1 x 2 + 1 2

Passo 2

Agora podemos separar nossa integral em 4 mais simples

∫ 3 x 3 + 1 x 2 x 2 + 1 2 d x = ∫ 1 x 2 d x - ∫ 1 x 2 + 1 d x + ∫ 3 x x 2 + 1 2 d x - ∫ 1 x 2 + 1 2 d x

E só precisamos resolver essas integrais

∫ 1 x 2 d x = - 1 x

∫ 1 x 2 + 1 d x = arctan ⁡ x

Para o caso da integral

∫ 3 x x 2 + 1 2 d x = 3 ∫ x x 2 + 1 2 d x  

Precisamos fazer uma substituição

u = x 2 + 1

d u = 2 x   d x

3 ∫ x x 2 + 1 2 d x = 3 2 ∫ 1 u 2 d u

= 3 2 .   - 1 u

Refazendo a substituição

3 ∫ x x 2 + 1 2 d x = - 3 2 x 2 + 1

Por último, para resolver a integral

∫ 1 x 2 + 1 2 d x

Precisamos utilizar uma substituição trigonométrica

x = tan ⁡ θ

d x = sec 2 ⁡ θ d θ

∫ 1 x 2 + 1 2 d x = ∫ sec 2 ⁡ θ tan 2 ⁡ θ + 1 2 d θ

Sabemos que tan 2 ⁡ θ + 1 = sec 2 ⁡ θ

∫ 1 x 2 + 1 2 d x = ∫ sec 2 ⁡ θ sec 4 ⁡ θ d θ

= ∫ 1 sec 2 ⁡ θ d θ = ∫ cos 2 ⁡ θ d θ

Podemos usar a substituição

cos 2 ⁡ θ = 1 2 + cos ⁡ θ 2

∫ 1 x 2 + 1 2 d x = ∫ 1 2 d θ + ∫ cos ⁡ θ 2 d θ

∫ 1 x 2 + 1 2 d x = 1 2 θ + sen ⁡ θ cos ⁡ θ

Fazendo as substituições de acordo com o triangulo trigonométrico teremos

∫ 1 x 2 + 1 2 d x = 1 2 arctan ⁡ x + x x 2 + 1

Passo 3

Finalmente, justando todas as integrais

∫ 3 x 3 + 1 x 2 x 2 + 1 2 d x = ∫ 1 x 2 d x - ∫ 1 x 2 + 1 d x + ∫ 3 x x 2 + 1 2 d x - ∫ 1 x 2 + 1 2 d x

∫ 3 x 3 + 1 x 2 x 2 + 1 2 d x = - 1 x - arctan ⁡ x - 3 2 x 2 + 1 - 1 2 arctan ⁡ x - x x 2 + 1 + C

∫ 3 x 3 + 1 x 2 x 2 + 1 2 d x = - 1 x - x + 3 2 x 2 + 1 - 3 2 arctan ⁡ x + C

Demorou, mas chegou, finalmente terminamos!

Resposta

Exercícios de Livros Relacionados

Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ 8 x 2 + 8 x + 2 4 x 2 + 1 2d x
Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ y 2 + 2 y + 1 y 2 + 1 2d y
Calcule.int (4)/(x^3 - x^2 - 2 x) d x
Faça uma substituição para expressar o integrando como uma função racional e então calcule a integral. ∫ s e n ( x ) cos 2 ⁡ x - 3 cos ⁡ x d x
Calcule a integralint (1)/((x - 2) (x^2 + 4)) d x