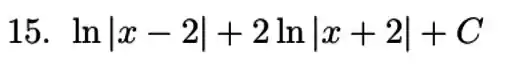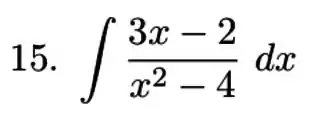
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Frações Parciais

Ver Teoria
Exercício 139123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Antes de começar, é importante verificar se o grau do denominador é maior que o do numerador. Nesse caso é fácil de ver que sim e pode continuar. Vamos lá para as nossas frações parciais!

Decompondo

x 2 - 4 = ( x + 2 ) ( x - 2 )

Então

3 x - 2 x 2 - 4 = A x + 2 + B x - 2

Passo 2

Fazendo com que as frações tenham o mesmo denominador teremos

3 x - 2 x 2 - 4 = A ( x - 2 ) ( x + 2 ) ( x - 2 ) + B ( x + 2 ) ( x + 2 ) ( x - 2 )

Se o denominador é o mesmo em ambos os lados da expressão podemos fazer

3 x - 2 = A x - 2 + B ( x + 2 )

3 x - 2 = A x - 2 A + B x + 2 B

3 x - 2 = x A + B - 2 A + 2 B

Agora, podemos usar aquele bizu! Quando chegamos na equação como agora, facilita substituir as raízes dos polinômios para zerar os termos. Nossas raízes são x = - 2 e x = 2 .

3 ( 2 ) - 2 = ( 2 ) A + B - 2 A + 2 B

6 - 2 = 2 A + 2 B - 2 A + 2 B

4 = 4 B

B = 1

Logo

A = 2

Nossa expressão na forma de frações parciais ficou

3 x - 2 x 2 - 4 = 2 x + 2 + 1 x - 2

Passo 3

Agora vamos voltar para a integral

∫ 3 x - 2 x 2 - 4 d x = ∫ 2 x + 2 d x + ∫ 1 x - 2 d x

∫ 3 x - 2 x 2 - 4 d x = 2 ∫ 1 x + 2 d x + ∫ 1 x - 2 d x

Para resolver a integral

∫ 1 x + 2 d x

Vamos utilizar a substituição

u = x + 2

d u = d x

Então ficamos com

∫ 1 x + 2 d x = ∫ 1 u d u

∫ 1 x + 2 d x = ln ⁡ u

Desfazendo a substituição

∫ 1 x + 2 d x = ln ⁡ x + 2

Fazendo a mesmíssima coisa com a outra integral, temos que

∫ 1 x - 2 d x = ln ⁡ x - 2

E substituindo na integral, ficamos com

∫ 3 x - 2 x 2 - 4 d x = 2 ln ⁡ x + 2 + ln ⁡ x - 2 + C

Não podemos esquecer a constante de integração! Prontinho.

Resposta

Exercícios de Livros Relacionados

Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ 8 x 2 + 8 x + 2 4 x 2 + 1 2d x
Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ y 2 + 2 y + 1 y 2 + 1 2d y
Calcule.int (4)/(x^3 - x^2 - 2 x) d x
Faça uma substituição para expressar o integrando como uma função racional e então calcule a integral. ∫ s e n ( x ) cos 2 ⁡ x - 3 cos ⁡ x d x
Calcule a integralint (1)/((x - 2) (x^2 + 4)) d x