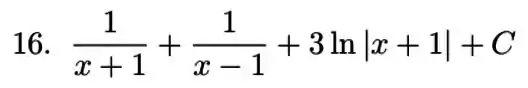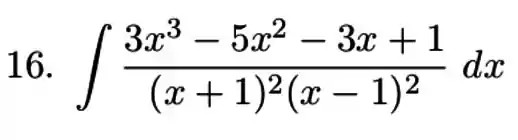
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Frações Parciais

Ver Teoria
Exercício 170123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Para começar precisamos decidir as frações parciais do nosso problema. Nesse caso, temos raízes múltiplas, então

3 x 3 - 5 x 2 - 3 x + 1 x + 1 2 x - 1 2 = A x + 1 + B x + 1 2 + C x - 1 + D x - 1 2

Se manipularmos um pouquinho

3 x 3 - 5 x 2 - 3 x + 1 x + 1 2 x - 1 2 = A x + 1 x - 1 2 x + 1 2 x - 1 2 + B x - 1 2 x + 1 2 x - 1 2 + C x - 1 x + 1 2 x + 1 2 x - 1 2 + D x + 1 2 x + 1 2 x - 1 2

3 x 3 - 5 x 2 - 3 x + 1 = A x + A x 2 - 2 x + 1 + B x 2 - 2 x + 1 + C x - C x 2 + 2 x + 1 + D ( x 2 + 2 x + 1 )

Manipulando isso mais um pouco

3 x 3 - 5 x 2 - 3 x + 1 = x 3 A + C + x 2 - A + B + C + D + x - A - 2 B - C + 2 D + A + B - C + D

Resolvendo chegamos em

A - C = 3

A + C = 3

Isso quer dizer que C = 0

B = - 1

D = - 1

Então ficamos com

3 x 3 - 5 x 2 - 3 x + 1 x + 1 2 x - 1 2 = 3 x + 1 - 1 x + 1 2 - 1 x + 1 2

Passo 2

Agora podemos separar nossa integral em 3 mais simples

∫ 3 x 3 - 5 x 2 - 3 x + 1 x + 1 2 x - 1 2 d x = ∫ 3 x + 1 d x - ∫ 1 x + 1 2 d x - ∫ 1 x - 1 2 d x

E só precisamos resolver essas integrais

∫ 3 x + 1 d x = 3 ∫ 1 x + 1 d x = 3 ln ⁡ x + 1

Para o caso da integral

∫ 1 x + 1 2 d x

Precisamos fazer uma substituição

u = x + 1

d u =   d x

∫ 1 x + 1 2 = ∫ 1 u 2 d u

= - 1 u

Refazendo a substituição

∫ 1 x + 1 2 d x = - 1 x + 1

Fazendo o mesmo para a integral

∫ 1 x - 1 2 d x = - 1 x - 1

Passo 3

Finalmente, justando todas as integrais

∫ 3 x 3 - 5 x 2 - 3 x + 1 x + 1 2 x - 1 2 d x = ∫ 3 x + 1 d x - ∫ 1 x + 1 2 d x - ∫ 1 x - 1 2 d x

∫ 3 x 3 - 5 x 2 - 3 x + 1 x + 1 2 x - 1 2 d x = 3 ln ⁡ x + 1 - - 1 x + 1 - - 1 x - 1 + C

∫ 3 x 3 - 5 x 2 - 3 x + 1 x + 1 2 x - 1 2 d x = 3 ln ⁡ x + 1 + 1 x + 1 + 1 x - 1 + C

Resposta

Exercícios de Livros Relacionados

Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ 8 x 2 + 8 x + 2 4 x 2 + 1 2d x
Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ y 2 + 2 y + 1 y 2 + 1 2d y
Calcule.int (4)/(x^3 - x^2 - 2 x) d x
Faça uma substituição para expressar o integrando como uma função racional e então calcule a integral. ∫ s e n ( x ) cos 2 ⁡ x - 3 cos ⁡ x d x
Calcule a integralint (1)/((x - 2) (x^2 + 4)) d x