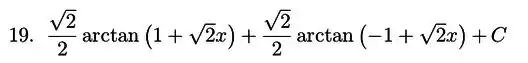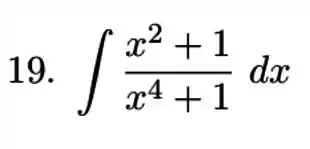
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Frações Parciais

Ver Teoria
Exercício 188123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Para começar, precisamos definir como fatorar nosso denominador para trabalhar com frações parciais. A decomposição pode ser

x 4 + 1 = ( x 2 + 2 x + 1 ) ( x 2 - 2 x + 1 )

Passo 2

Separando em frações parciais

x 2 + 1 x 4 + 1 = A x 2 + 2 x + 1 + B x 2 - 2 x + 1

Colocando num mesmo denominador

x 2 + 1 x 4 + 1 = A ( x 2 - 2 x + 1 ) ( x 2 + 2 x + 1 ) ( x 2 - 2 x + 1 ) + B ( x 2 + 2 x + 1 ) ( x 2 + 2 x + 1 ) ( x 2 - 2 x + 1 )

x 2 + 1 = A x 2 - A 2 x + A + B x 2 + B 2 x + B

x 2 + 1 = ( A + B ) x 2 + ( - A 2 + B 2 ) x + A + B

A + B = 1

2 - A + B = 0

A = B

A = B = 1 2

Então ficamos com

x 2 + 1 x 4 + 1 = 1 2 ( x 2 + 2 x + 1 ) + 1 2 ( x 2 - 2 x + 1 )

Passo 3

Aplicando na nossa integral ficamos com

∫ x 2 + 1 x 4 + 1 d x = ∫ 1 2 ( x 2 + 2 x + 1 ) d x + ∫ 1 2 ( x 2 - 2 x + 1 ) d x

∫ x 2 + 1 x 4 + 1 d x = 1 2 ∫ 1 ( x 2 + 2 x + 1 ) d x + 1 2 ∫ 1 ( x 2 - 2 x + 1 ) d x

Passo 4

Agora, vamos resolver as integrais resultantes.

∫ 1 x 2 + 2 x + 1 d x

Para resolver essa integral, facilita se completarmos um quadrado no denominador.

x 2 + 2 x + 1 = x + 2 2 2 + 1 2

Então

∫ 1 x 2 + 2 x + 1 d x = ∫ 1 x + 2 2 2 + 1 2 d x

Podemos ainda dar mais uma rearranjada:

∫ 1 x + 2 2 2 + 1 2 d x = ∫ 1 1 2 2 x + 2 2 2 + 1 d x =

= ∫ 2 2 2 x + 2 2 2 + 1 d x = ∫ 2 2 x + 2 2 2 + 1 d x =

= ∫ 2 2 x + 1 2 + 1 d x

E podemos utilizar a substituição

u = 2 x + 1

d u = 2 d x

Daí

∫ 2 2 x + 1 2 + 1 d x = ∫ 2 u 2 + 1 d u

= 2 ∫ 1 u 2 + 1 d u

= 2 arctan ⁡ u

Refazendo a substituição

∫ 2 2 x + 1 2 + 1 d x = 2 arctan ⁡ 2 x + 1

Fazendo exatamente o mesmo procedimento, chegamos em

∫ 1 x 2 - 2 x + 1 d x = 2 arctan ⁡ 2 x - 1

Passo 5

Por fim, vamos juntar nossos resultados na expressão em frações parciais que encontramos lá no passo 3.

∫ x 2 + 1 x 4 + 1 d x = 1 2 ∫ 1 ( x 2 + 2 x + 1 ) d x + 1 2 ∫ 1 ( x 2 - 2 x + 1 ) d x

∫ x 2 + 1 x 4 + 1 d x = 1 2 2 arctan ⁡ 2 x + 1 + 1 2 2 arctan ⁡ 2 x - 1

∫ x 2 + 1 x 4 + 1 d x = 2 2 arctan ⁡ 2 x + 1 + 2 2 arctan ⁡ 2 x - 1

Resolvido!

Resposta

Exercícios de Livros Relacionados

Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ 8 x 2 + 8 x + 2 4 x 2 + 1 2d x
Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ y 2 + 2 y + 1 y 2 + 1 2d y
Calcule.int (4)/(x^3 - x^2 - 2 x) d x
Faça uma substituição para expressar o integrando como uma função racional e então calcule a integral. ∫ s e n ( x ) cos 2 ⁡ x - 3 cos ⁡ x d x
Calcule a integralint (1)/((x - 2) (x^2 + 4)) d x