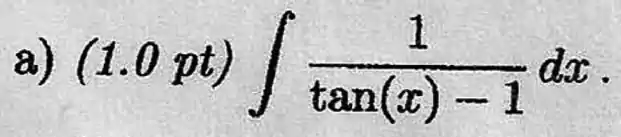
Passo 1
Aqui, vamos começar abrindo a substituindo a tangentepor uma variável . Não tem nada que me indique usar nenhum método de integração específico, então vou começar forçando essa substituição e ver se melhora a minha vida:
Acontece que não temos esse na integral pedida, então vamos escrevê-lo em função do que temos, que é só . Temos que e , logo:
Beleza! Então vamos usar isso na integral:
Passo 2
Vamos então usar o método das frações parciais para resolver esse cara:
Igualando cada potência de de um lado e de outro, obteremos o seguinte sistema:
De onde achamos
Teremos, portanto:
Passo 3
A primeira integral vai sair por substituição simples:
A segunda também (com e ):
A última é a integral do arco tangente, sai de primeira:
Com isso,
Passo 4
Agora desfazemos a substituição, vamos ficar com o seguinte:
Sendo que temos uma composta de funções que são inversas entre si, , que acaba sendo a mesma coisa que . O resultado final fica assim:
Resposta
Ei, a resposta está no passo a passo :)