4) Calcule cada uma das integrais abaixo.
c)
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!

Antes de sairmos resolvendo essa integralzinha aqui, você já parou pra pensar em que método vamos usar pra fazer isso?

Antes de tudo vamos observar a nossa função que será integrada:
Aqui, vamos observar que podemos fazer uma divisão de polinômios, já que no numerador temos elevado à terceira potência, e que no denominador temos uma expressão também com !
Vamos lá fazer essa divisão então!
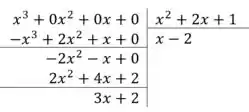
Como não temos uma divisão de resto 0, a resposta final será o quociente somado com o resto dividido pelo divisor! Isso é uma regrinha, beleza?
Vamos reescrever a nossa integral então:
Olha só que legal! Temos agora uma expressão que pode ser dividida em várias integrais, já que temos soma e subtração!
Vamos ficar com algo mais ou menos assim então:
As duas primeiras integrais são muuuito simples de resolver, então já vamos colocar o resultado delas aqui!
Agora para a terceira integral, como temos aquela carinha ali no denominador, podemos usar o método de integração por frações parciais, onde integraremos membro a membro! Mas como fazemos isso?
Bora lá resolver ela no próximo passo!
Passo 2
Antes de tudo, como no denominador o está elevado â segunda potência, devemos primeiramente fatorá-lo:
Para cada fator no denominador, criaremos uma fração usando o fator como denominador e um valor desconhecido () como numerador.
Nesse caso, como o fator no denominador está ao quadrado, teremos algo do tipo:
Mas e agora? O que eu faço com essa integral?
Agora devemos encontrar o valor de e de ! Bora lá então!
Passo 3
Para definirmos os valores de e , vamos multiplicar o denominador da função original em todos os termos da igualdade. Desse modo, o lado esquerdo da igualdade será , e a partir disso poderemos achar os valores que queremos.
Relembrando a função na qual trabalharemos:
Multiplicando:
Agora que temos essa expressão simplesinha, podemos aplicar distributiva:
Agora com isso, podemos estabelecer um sistema de equações.
Substituindo em :
Pronto! Encontramos os valores de A e B!
Passo 4
Olha só! Conseguimos finalmente transformar a nossa função original em uma função com frações parciais:
Mas e agora? Faço o que com isso?

Calma! Antes de tudo vamos observar que temos a soma de duas frações. Isso quer dizer que podemos dividir a integral entre essas somas:
Outra coisa que podemos perceber aqui, -1 e 3 são constantes nas duas integrais. Então elas podem ser retiradas da integral:
Agora, como temos duas integrais, vamos encontrar cada uma separadamente, e depois somar o seu resultado!
Passo 5
Resolvendo a primeira integral, vamos ter que:
Para resolvê-la, vamos usar o método da substituição em . Então, adotaremos e .
Sendo assim:
Como está ao quadrado, podemos transformar isso em:
Essa integral é uma integral conhecida! Portanto, podemos colocar o resultado dela diretamente:
Retornando o valor de :
Agora vamos resolver a segunda integral:
Aqui também podemos resolver utilizando o método da substituição . Pra esse caso, adotaremos então e
Essa integral também é conhecida:
Retornando o valor de :
Pronto! Já temos o valor da última integral!!
Passo 6
Por fim, substituindo o valor da terceira integral na nossa equação lá do passo 1, vamos ter:
Organizando melhor o nosso resultado, temos:
Ufa!! Terminamos!

Pra essa questão é isso pessoal! Bora pra mais uma?