UFCG, Sem Campus, Cálculo Diferencial e Integral III, Listas - Profª Pamella Queiroz - Lista 1 - 2022.1, Questão 1.1gh
Em cada caso identifique e represente graficamente o domínio da função .
Passo 1
Oiie, tudo bem?
O enunciado nos dá duas funções, sendo elas
e, precisamos determinar o domínio destas funções! Isso significa, analisar as funções para obter limitações nos valores de , o caminho costuma sempre ser analisar expressões algébricas que surgem devido a restrições dadas pelo formato da função! Vamos começar com a primeira alternativa! Vem comigo!
Passo 2
Temos que determinar o domínio da função
O argumento do arcocosseno deve estar delimitado entre , portanto, temos que
Isso nos dá duas retas
e
Ou seja, o domínio é tal que
que pode ser representado no plano como
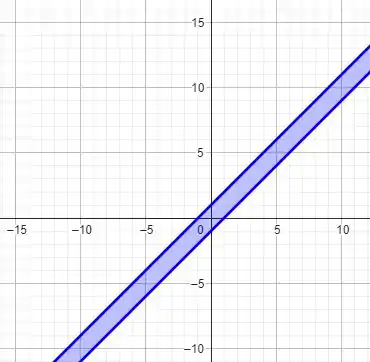
Vamos fazer a outra agora! Bora lá!
Passo 3
Temos a função
Não podemos ter valores negativos dentro da raíz para mantermos nosso domínio real! Portanto, temos que
essa condição é válida quando temos que
e
ou
e
ou seja, o domínio é dado pela intersecção de dois conjuntos
A questão é isso! Te vejo na próxima! Tchauzinho!