UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 1, Questão 4c
4. Encontre o domínio e esboce o gráfico da função.
c)
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema, queremos obter o domínio e o esboço do gráfico da função .
Parece tranquilo? 🤔
Para obter o domínio de uma função, podemos fazer uma analogia com uma receita de uma pizza...
Em uma receita, adicionamos os ingredientes na massa e levamos ao forno.
O domínio de uma função é todos os valores possíveis que a função pode adquirir na variável, ou seja, os possíveis valores para . Assim como os ingredientes da pizza pode ser considerado como o domínio da pizza.
Já para obter o gráfico de uma função, podemos obter alguns pontos dela e estimar o comportamento da função entre os pontos.
Sacou? Bora começar! 😁
Passo 2
Primeiro vamos obter o domínio de , pra isso, vamos analisar a função.
Na função vemos que há restrições para , já que raízes de números negativos não existem no conjunto dos números reais.
Portanto, o que está dentro da raiz precisa ser maior que , ou seja
Logo, o domínio de é todos os valores reais maiores ou iguais a .
Legal, né? 😎
Passo 3
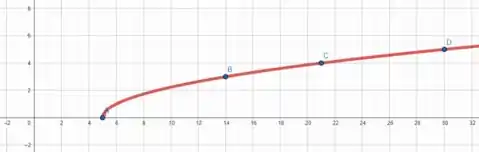
Agora para esboçar o gráfico de vamos estimar alguns pontos e ver como a função se comporta
Para ...
Para
Para
E para
Perceba que a função cresce a uma velocidade muito baixa, ou seja
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
