1) Determine o domínio e a imagem das funções abaixo
j)
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês?

Bora lá resolver mais uma questão!!
Nesse exercício precisamos encontrar o domínio e a imagem da função dada pelo enunciado. Bom, qual foi a função que ele nos deu nessa letra j?
Beleza, então precisamos calcular o domínio e a imagem desse g(x) que ele nos deu.
Legal, mas o que é domínio e imagem? Como encontramos esses valores?
Bem, para entendermos o que é um domínio e imagem, precisamos antes definir o que é função. Conhecemos como função uma relação entre dois conjuntos A e B em que, para todo elemento do conjunto A, existe um único correspondente no conjunto B. A “ferramenta” que transforma os elementos do conjunto A em um elemento do conjunto B é o que chamamos de função. Vamos pensar em uma imagem que nos ajude a entender de forma mais clara essa ideia.
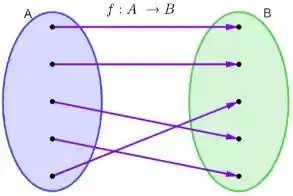
Show, então vamos pensar que o conjunto B seja um bolo. O conjunto A é dado pelos ingredientes. Então, nesse caso, o que seria nossa função? Bom, a função é a receita que precisaremos seguir pra fazer o bolo, a partir dos ingredientes. Entendido, pessoal?
Assim já definimos quem é o domínio. O domínio é o conjunto numérico formado pelos valores que pode assumir na nossa função. Então, ele seria cada um dos ingredientes possíveis pra fazermos o bolo. Vamos pensar, será que pra fazer um bolo de cenoura, seria legal colocarmos mostarda? Hmmm, acho que não, né? Por isso o domínio é importante. Ele nos auxilia a entender quais valores nossa variável da função pode admitir.
Já a imagem é um subconjunto do contradomínio formado por todos os elementos que correspondem a algum elemento do domínio. Calma, sei que essa frase cheia de definições pode assustar. Vamos traduzir ela aqui pra nossa língua hahahaha. A imagem é dada por Ou seja, ttodos os valores possíveis que sairão da nossa “ferramenta” e, formarão a nossa imagem. Ou seja, é cada pedacinho de ingrediente que se transforma no bolo.
Muito legal, não é? Então bora calcular!
Passo 2
Como vimos no Passo 1, o domínio é formado pelos possíveis valores de . Aqui procuramos se há algum valor de que torna a função impossível de ser resolvida. Ou seja, se tivermos a mostarda no meio dos ingredientes, o resultado do bolo não é legal. Na nossa função, será que isso acontece? É isso que precisaremos olhar aqui. Se existe algum valor de x para o qual nossa função não seja possível de acontecer.
Vamos juntos? Bora!!!
Olhando para essa nossa função:
, Hmm, aqui percebemos que é uma fração. Para que uma fração exista, quais são os principais requisitos? Bom, o numerador não apresenta nenhuma restrição. E o denominador? Temos que o denominador precisa ser diferente de 0. Isso porque não é possível dividirmos uma coisa por 0 vezes, né? e avaliamos automaticamente o seguinte:
O numerador não apresenta nenhuma restrição.
Já o denominador, partiríamos para a análise do denominador ser diferente de .
No nosso denominador da função, a gente tem a seguinte expressão:
Show, precisamos encontrar, então, quais são os valores de para que essa expressão seja diferente de 0. Mas olha só, parece que temos uma expressão de exponencial, com no expoente. Qualquer valor que colocarmos em , dará diferente de 0 né? Isso porque, lembrem-se: expressões exponenciais nunca assumem o valor de 0 quando a variável está em seu expoente.
Porém, como temos uma de , ela nunca assumirá o valor igual a .
E agora? O que fazemos com o domínio? O que ele é?
Bom, como encontramos que não existe valor de para que nossa função não exista, então o nosso domínio pode ser dado por qualquer valor de . E encontramos um bolo mágico: aquele que fica bom com qualquer ingrediente que colocamos hahahaha.
Portanto, o domínio da nossa função pode ser escrito dessa forma aquié:
O domínio são todos os valores de pertencentes aos números reais.
Passo 3
Agora para a imagem, vamos observar os possíveis resultados da nossa função. Qual é nossa função mesmo? Hmm, é essa aqui:
Da mesma forma que vimos no Passo 2, não há valores de impossíveis. Ou seja, qualquer valor de domínio nos dará uma função existente. É o bolo mágico! Logo, todos os números reais fazem parte da imagem. E assim, encontramos que pra nossa função , a imagem pode ser dada por::
E é isso, galerinha!! Encontramos aqui que tanto o domínio quanto a imagem estão dentro dos valores reais. Tudo certinho?
Morri mas passo bem depois dessa questão longa!

Mas a sensação de conseguir fazer é bom demais, fala aí! Vamos pra próxima então?