USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.1c
1.1. Para cada função dada, determine o domínio e faça um esboço dele:
c)
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema queremos obter o domínio da função e obter um esboço do seu gráfico.
Parece tranquilo? 👀
Para obter o domínio de uma função, temos que analisar a função em si e se perguntar quais os possíveis valores as variáveis podem admitir para que a função seja definida no espaço real.
Legal, né? 😊
Já para obter o gráfico da função, podemos usar algumas arte manhas, como por exemplo obter algumas curvas de níveis da função fazendo e definindo algum valor para onde seja definido, ou também fixar alguma das variáveis a um constante e esboçar seu gráfico em duas dimensões no plano onde a variável foi fixada.
Entendeu? Bora lá! 😉
Passo 2
Analisando a função , temos que para obter o domínio, temos que identificar como a função pode ser definida.
Primeiramente, vemos que que a função se trata de uma fração e o que sabemos é que o denominador de uma fração deve ser diferente de para que essa fração exista.
Porém, o denominador dessa fração é dado por e sabemos que o conteúdo de uma raiz tem que ser maior ou igual a para que haja um resultado real.
Com isso, para que a função exista, o conteúdo da raiz tem que ser maior que
Escrevendo isso de uma forma mais bonitinha, temos
Tranquilo até aqui? 😉
Passo 3
Agora para esboçar o gráfico de , podemos usar os métodos que vimos no passo 1.
Começando pelo método dos níveis, temos que fazer , onde representa um nível em (uma altura no eixo ).
Para , temos
Para
Para
Esboçando cada curva em sua respectiva altura , temos
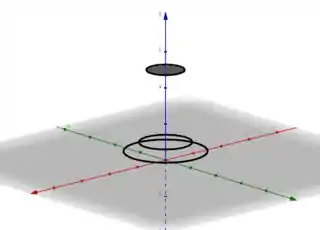
Assim podemos perceber que quanto maior , mais próximo de nos estamos e quando diminui, o raio da circunferência aumenta.
Portanto podemos esboçar o gráfico de como
Fim! Iae, o que achou? Responde Aí! 😁