UFCG – Cálculo Diferencial e Integral I – Atividade Avaliativa 3 (AV3) – Parte 1 – 2022.2 – Questão 3a.
- Seja a função , determine:
- O domínio da função e suas raízes:
Passo 1
Fala aí!!! Tudo belezinha com você? Bora desenvolver essa questão comigo?!
Bom, a questão dá pra gente a função
e pede para gente dizer qual o domínio dela e quais são suas raízes. Então nós vamos dividir essa resolução em duas parte. Na primeira parte nós iremos encontra o domínio, que são os valores onde a função está definida, e na segunda parte nós iremos encontrar as raízes, que são os pontos onde a função corta o eixo .
Vem comigo que vamos fazer isso juntos.
Passo 2
Para descobrir o domínio da nossa função precisamos pensar se existe algum valor que o não pode assumir. Isso porque o domínio da função é exatamente o conjunto de valores que podemos colocar no lugar de .
Temos vários casos de funções que ficam indeterminadas em valores específicos de , mas esse não é o caso da função do nosso problema. Observe-a:
Como ela é uma função polinomial, podemos colocar o valendo qualquer coisa que conseguimos calcular sem grandes esforços o valor da função. Isso significa que nossa função está definida em todos os valores reais de . E escrevemos seu domínio deste modo:
Show. Essa parte foi de boas. Agora vamos encontrar as raízes da função.
Passo 3
Chamamos de raízes da função os valores de que fazem com que a função seja igual a zero. Isso quer dizer que para encontrar as raízes de qualquer função, basta igualar ela a zero e resolver a equação que iremos obter.
Um modo bem rápido de resolver essa equação é colocando o em evidência:
Isso porque fomos capazes de escrevê-la como um produto entre e o . E um produto só poderá ser igual a zero, se algum de seus fatores for igual a zero. Assim temos duas possibilidades.
Podemos ter:
O que nos dá duas raízes iguais a zero
e
Ou podemos ter:
Nos dando a terceira raiz
Obs: Nós encontramos três raízes porque a nossa função é uma função de terceiro grau, beleza?
E esses são os pontos onde o gráfico da função corta o eixo . Também podemos vê-lo através do gráfico da função. Veja só:
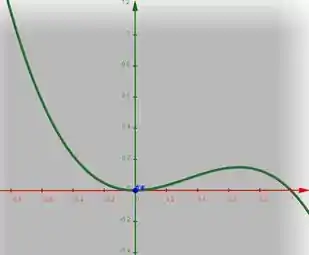
E prontinho. Problema resolvido. 😊
Partiu próxima?!
Resposta
Raízes e