UFSCar; Cálculo I – 1ª Lista de exercícios - Revisão de funções – Ex. 1h
1) Determine o domínio e a imagem das funções abaixo
h)
Passo 1
Alooo, �� aqui que temos alunos aplicadíssimos e animados com essa questão??
Ebaa, é sim!! Vamos então…
Nesse exercício precisamos encontrar o domínio e a imagem da função dada pelo enunciado.
Legal, mas o que é domínio e imagem? Como encontramos esses valores?
Bem, para entendermos o que é um domínio e imagem, precisamos definir o que é função. Conhecemos como função uma relação entre dois conjuntos A e B em que, para todo elemento do conjunto A, existe um único correspondente no conjunto B. A “ferramenta” que transforma os elementos do conjunto A em um elemento do conjunto B é o que chamamos de função.
Assim já definimos quem é o domínio. O domínio é o conjunto numérico formado pelos valores que pode assumir na nossa função.
Já a imagem é um subconjunto do contradomínio formado por todos os elementos que correspondem a algum elemento do domínio. Ou seja, todos os valores possíveis que sairão da nossa “ferramenta”, formarão a nossa imagem.
Muito legal, não é? Então bora calcular!
Passo 2
Como vimos no Passo 1, o domínio é formado pelos possíveis valores de . Aqui procuramos se há algum valor de que torna a função impossível de ser resolvida.
Como estamos falando de uma função exponencial com base dentro da função tangente, de cara teremos uma exceção. A função tangente tem uma assíntota vertical cíclica, ou seja, um ponto onde o gráfico tem um limite, se repetindo com o produto de um número inteiro. Ficou bem confuso, né?
Calma, é mais simples do que parece. A função tangente possui assíntota toda vez que:
Obs.: nesse argumento pode ser qualquer número inteiro e é ele que gera a repetição “cíclica” da função.
Uma forma visual de demonstrar esse argumento é com o gráfico de :
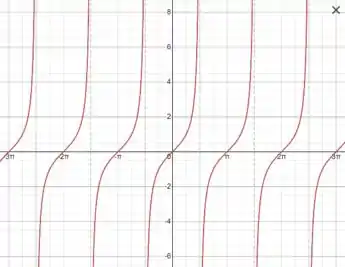
Agora que sabemos um ponto que a função tangente não é definida, podemos avaliar o seguinte:
Aqui encontraremos valores de que serão indefinidas na nossa função. Resolvendo:
Como encontramos a exceção, definimos o nosso domínio:
O domínio de é qualquer diferente de , para todo .
Passo 3
Agora para a imagem, vamos observar os possíveis resultados da nossa função.
Pensando nos resultados possíveis de uma função tangente normal, todos os valores de são possíveis como imagem.
E como também não possui exceções de imagem, podemos dizer que:
A imagem é para qualquer pertencente aos números reais.
Pra essa questão é isso, pessoal! Mais fácil do que você imaginou, fala aí!
Vamos juntos resolver mais uma?