Um projétil é lançado de uma altura com uma velocidade , como ilustrado pela figura a seguir:
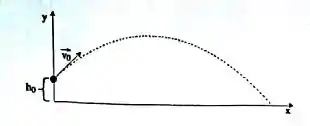
Sabendo que esse projétil está submetido à aceleração da gravidade (, a sua trajetória pode ser parametrizada da seguinte maneira:
Passo 1
Da física, sabemos (nem sempre lembramos, mas sabemos) que a função horária da posição, num movimento com aceleração uniforme, e dado por:
E no eixo y teremos um movimento desse tipo.
No nosso caso, sabemos que a posição inicial do nosso projétil é:
Que a velocidade inicial no eixo y é a componente y da velocidade inicial, vamos chamar de .
Ainda, sabemos que a aceleração a que ele está submetido, na direção vertical, é simplesmente a aceleração da gravidade:
Então vamos ficar com:
Passo 2
Para o eixo horizontal, teremos um movimento uniforme. Do tipo:
Em que é a componente x da velocidade inicial, vamos chamar de . Então:
Passo 3
Agora, somando tudo:
Repare que eu posso escrever:
E aí vai ficar: