UFSCAR - Sem Campus - Cálculo 1 - Listas - Teste 9 - Listas de Estudos Cálculo 1 - UFSCAR - Lista 1 - Versão 2 - Questão 5 - Alternativa a
Considere a função dada por .
Determine e .
Passo 1
Oiie, tudo bem?
O enunciado nos dá a seguinte função
e, nesta alternativa, precisamos identificar o seu domínio e a sua imagem . Ou seja, precisamos encontrar limitações sobre o valor de para determinar o domínio, e a partir destas limitações analisar quais são os resultados possíveis da função, o que chamamos de . Vamos analisar esta função! Belezinha?
Passo 2
A função é um polinômio de grau . Todo polinômio têm como domínio todos os valores reais, portanto, podemos dizer que
sem qualquer limitação! Mas e a imagem? Podemos fazer um esboço jogando diferentes valores para e calculando , você irá notar que isso gera a seguinte parábola
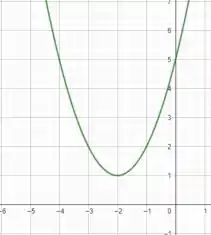
Note que não há nenhuma limitação sobre a imagem, ou seja
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e