UFSCar; Cálculo I – 1ª Lista de exercícios - Revisão de funções – Ex. 2a
2) Determine o domínio e esboce o gráfico das funções
a)
Passo 1
Opa pessoas lindas desse mundãooo do Responde Aí!! Leu esse enunciado e ficou um pouco confuso?
Calma, vamos resolver juntos com muito amor e carinho hehehehehe. Vamos que vamos!!
Nesse exercício precisamos encontrar o domínio e construir o gráfico da função dada pelo enunciado.
Legal, mas o que é domínio de uma função? E como se constrói um gráfico?
Bem, para entendermos o que é um domínio, precisamos definir o que é função. Conhecemos como função uma relação entre dois conjuntos A e B em que, para todo elemento do conjunto A, existe um único correspondente no conjunto B. A “ferramenta” que transforma os elementos do conjunto A em um elemento do conjunto B é o que chamamos de função.
Assim já definimos quem é o domínio. O domínio é o conjunto numérico formado pelos valores que pode assumir na nossa função.
Já para a construção do gráfico, usaremos métodos específicos para cada função, levando em consideração algumas simplificações possíveis e características do grau e forma da função.
Muito legal, não é? Então bora calcular!
Passo 2
Como vimos no Passo 1, o domínio é formado pelos possíveis valores de . Aqui procuramos se há algum valor de que torna a função impossível de ser resolvida.
Olhando para essa nossa função, percebemos que todos os valores reais servem. Em outras palavras, não há nenhum valor para que torne a função imprópria.
Ou seja, o nosso domínio são todos os valores reais:
Passo 3
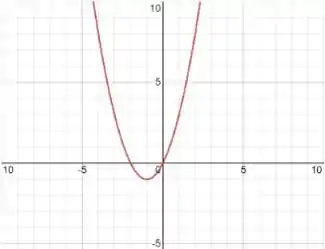
Agora, para o gráfico, vamos começar identificando qual é o tipo dessa função.
Nesse exercício, temos uma função do segundo grau. Isso fica claro quando observamos . Como é uma função do segundo grau, o formato do gráfico será uma parábola. E como o número que acompanha o termo quadrado é positivo (imagine que existe o número multiplicando ), a concavidade desse gráfico será virada para cima.
Agora precisamos encontrar alguns pontos que nos ajudem a construir esse gráfico.
Como estamos falando de uma parábola, podemos calcular seu vértice. Esse é o ponto mais abaixo da parábola, onde há a mudança de sentido do gráfico.
Para encontrarmos o do vértice podemos utilizar:
Esses termos e são os números que acompanham os termos quadráticos e lineares da nossa função, respectivamente. Então e .
Agora que sabemos que em temos o vértice, vamos encontrar seu .
Legal! O ponto é o vértice.
Agora podemos considerar . Assim encontraremos em quais pontos o gráfico corta o eixo .
Então, nos pontos e o gráfico corta o eixo .
Só para referenciar melhor nosso gráfico, podemos considerar e assim encontraremos outros dois pontos pertencentes ao gráfico:
Reescrevendo:
Resolvendo por soma e produto:
Portanto os pontos e fazem parte do gráfico. Agora ficou fácil criar o gráfico:
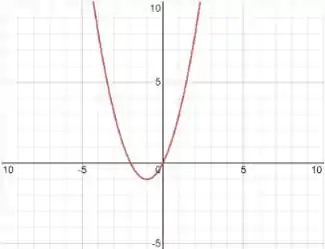
Uhuuuuul!! Terminamos essa questão monstrengozinha!
E aí?! O que acharam?
Prontos pra fazer mais uma e ficar com essa sensação top de que conseguimos? Hehehehe
Resposta
