UFSCar; Cálculo I – 1ª Lista de exercícios - Revisão de funções – Ex. 2g
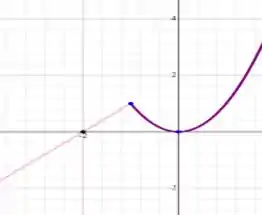
2) Determine o domínio e esboce o gráfico das funções
g)
Passo 1
Alooo, é aqui que temos alunos aplicadíssimos e animados com essa questão??
Ebaa, é sim!! Vamos então…
Bem, para entendermos o que é um domínio, precisamos definir o que é função. Conhecemos como função uma relação entre dois conjuntos A e B em que, para todo elemento do conjunto A, existe um único correspondente no conjunto B. A “ferramenta” que transforma os elementos do conjunto A em um elemento do conjunto B é o que chamamos de função.
Assim já definimos quem é o domínio. O domínio é o conjunto numérico formado pelos valores que pode assumir na nossa função.
Já para a construção do gráfico, usaremos métodos específicos para cada função, levando em consideração algumas simplificações possíveis e características do grau e forma da função.
Muito legal, não é? Então bora calcular!
Passo 2
Como vimos no Passo 1, o domínio é formado pelos possíveis valores de . Aqui procuramos se há algum valor de que torna a função impossível de ser resolvida.
Não há nenhuma restrição para os valores de que torna a função impossível de ser calculada. Mesmo com a função dividida em duas fases, todos os valores de servirão. Então o domínio da função são todos os números reais:
Passo 3
Agora, para o gráfico, vamos começar identificando qual é o tipo dessa função.
Essa é uma função dividida em duas fases. Isso significa que para determinados valores de o gráfico terá um comportamento e para outros valores de terá outro comportamento.
Vamos começar avaliando , que é a função para os valores menores ou iguais a .
Essa função é uma reta. E para traçarmos uma reta precisamos definir dois pontos.
Um ponto que sabemos é que é justamente o ponto onde a função muda de fase. Basta calcularmos para sabermos o primeiro ponto da reta:
Então o ponto faz parte da reta.
Podemos definir para encontrarmos outro ponto da reta:
Então o ponto faz parte da reta.
Agora vamos considerar a fase do gráfico.
Essa função tem seu vértice no ponto . Além disso é uma função simétrica. Podemos definir outros dois pontos para termos a referência do gráfico.
Por exemplo, vamos encontrar os pontos de para :
Então os pontos e fazem parte do gráfico.
Agora já temos tudo o que precisamos para desenhar o gráfico:
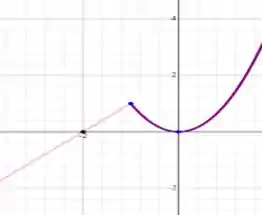
Morri mas passo bem depois dessa questão longa!
Mas a sensação de conseguir fazer é bom demais, fala aí! Vamos pra próxima então?
Resposta
