Encontre o domínio, a imagem e esboce o gráfico do domínio da função:
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função de duas variáveis , e pediu pra gente encontrar o domínio, junto com seu gráfico, e a imagem dela. Mas como a gente pode determinar o domínio da função?
Lembra que pra determinar o domínio, nós olhamos primeiro para as restrições da função? Quer dizer, nós olhamos para os valores que a função não pode assumir. Isso porque o domínio da função, no caso da função de duas variáveis, é a região do plano onde ela está definida.
Então, a gente só tem que garantir que o denominador da fração não pode ser zero e que dentro da raiz quadrada não pode ter número negativo, na nossa função:
E a imagem vai ser o conjunto de todos os valores que a função assume para cada ponto dentro do domínio, ou seja:
Então, vamos lá!
Passo 2
Pra definir o domínio, como a gente falou lá em cima, a gente precisa garantir que o denominador da fração não pode ser zero e que dentro da raiz quadrada não pode ter número negativo. Matematicamente fica assim:
Logo,
Ou, se a gente ler da direita pra esquerda fica assim:
Repara que essa é uma equação de circunferência, beleza? Essa circunferência é centrada na origem e tem raio . Mas a gente tá interessado apenas na parte interna da circunferência, porque é menor do que . Então nosso domínio pode ser representado assim:
E graficamente:
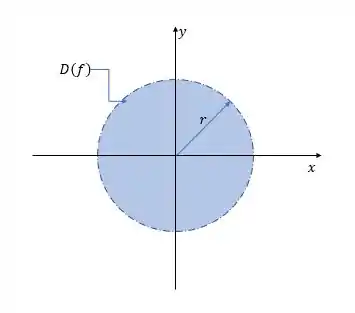
Passo 3
Agora vamos avaliar a imagem da nossa função. Sabendo que a imagem é um conjunto de valores correspondente aos pontos do domínio, nós podemos dizer que pertence a imagem da função. Ou seja:
Mas , então temos:
Se a gente elevar os dois lados , a gente inverte as frações e ficamos com:
Agora vamos elevar os dois lados ao quadrado:
Vamos passar o pro outro lado e multiplicar todo mundo por :
Mas quem é esse Bom, nós sabemos que ele vai ser um número positivo, porque ele tá elevado ao quadrado. Mas será que ele pode ser qualquer número positivo? E se ele for um número muito grande?
Pensa comigo, se o for um número muito grande, então vai ser um número bem pequeno, né? Ou seja, ele vai tender a zero, quando tender a infinito, e aí nós iríamos ter apenas:
E se o for um número positivo, mas muito pequeno? Bom, aí a gente teria menos um número muito grande, porque vai me dar um número grande. E aí o que acontece? Aí nós teríamos um número negativo, o que não pode acontecer, porque a soma de dois quadrados () precisa ser um número positivo.
Tá, e se aquilo tudo ali do lado direito fosse zero? A gente teria isso aqui:
Vamos isolar o :
Então, o que a gente pode concluir? Que o nosso pode ser um número tão grande quanto a gente queira, mas se a gente for diminuindo o valor dele, ele só pode chegar a . Isso porque, se for menor que , vai dar um número negativo (e isso não pode acontecer, como a gente viu ali em cima).
Analisando tudo isso, a gente pode dizer que:
Então, como , nossa imagem vai tá definida assim:
Fechou?!
Até a próxima, galera! 😉