Para a função com fórmula
a) Determine o domínio máximo dessa função.
b) Esboce as curvas de nível , e para essa função no mesmo plano.
c) Existe um ponto (a,b) no qual essas 3 curvas de nível parece se encontrar. Encontre esse ponto e explique como é possível.
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! Primeiro, no item a), vamos determinar o domínio máximo dessa função:
Mas veja, o domínio dessa função são todos os possíveis (porque não temos quase nenhuma restrição pra ela), exceto com uma única restrição. Essa restrição é para o dominador ser igual a 0. Porque aí gera uma indeterminação e a função não existe nesse ponto. Logo o domínio é:
Passo 2
Show, agora precisamos esboçar 3 curvas de nível pra essa função. Você sabe como são definidas as curvas de nível? Elas são as curvas que fazem o contorno da região da função . Nós encontramos elas a partir de um , que ao substituir o por algum inteiro, temos:
E por exemplo, ao aplicarmos o ponto , como a questão pede, temos:
Isso implica que:
Esboçando essa reta no gráfico, temos:
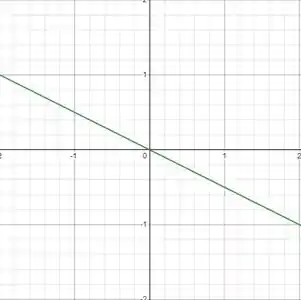
Semelhantemente, para , obtemos a seguinte reta:
Isso implica que:
Representando graficamente:
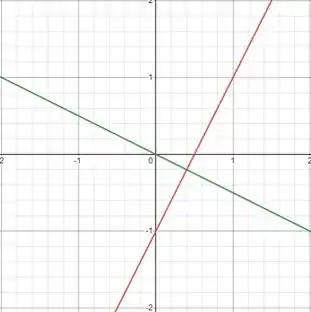
Belezinha, tamo quase lá. Pra gente finalizar, aplicando :
Isso implica que:
Representando no nosso gráfico:
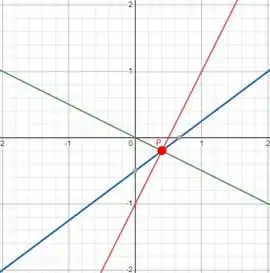
E como o item c) deu o spoiler, a gente tem um ponto onde essas 3 curvas de nível parece se encontrar.
Passo 3
Show, bora encontrar esse ponto então. Mas, olha que sacada interessante, se a gente notar as curvas de nível como:
Elas podem ser representadas por: (lembrando que a notação “(3)” significa a equação (3), que eu citei nesse passo)
Portanto, isso se caracteriza como um sistema redundante. Ou seja, basta relacionarmos a eq (3) com a (2), ou a eq (3) com a (1), ou a eq (2) com a (1). Não precisamos relacionar 3 equações. Logo, para:
Encontramos que:
Isso implica que o ponto nas coordenadas é representado por:
Passo 4
Belezura... mas como isso é possível? Estamos literalmente pegando 3 curvas que estão em “altitudes diferentes”:
E ainda assim elas se encontram em um ponto. Isso a primeira vista, não faz sentido mesmo. E sabe o mais estranho ainda? Se você aplicar esse ponto
Na região do domínio onde a função não é determinada:
Obtemos:
Ou seja, o ponto P nem pertence ao domínio da função, e ainda assim faz com que 3 curvas de nível se encontrem nele.

Passo 5
Calma little padawan. A figura do passo 2 representa somente o ponto aonde as curvas de nível, ao serem projetadas no plano , se encontram. Ela não representa um ponto que de fato esteja contido na função. Ou seja, ainda é indeterminado na região, somente as curvas de nível se tocaram propositalmente nesse ponto, pra tentar pregar uma peça no aluno e fazer com que a gente aprenda mais esse conceito de curva de nível. Felizmente, o aluno do R.A é preparado pra qualquer pegadinha HAHAHAHA.

E é isso! WE DID IT!!! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você