UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 1, Questão 5c
5. Encontre uma fórmula para a função descrita e obtenha seu domínio.
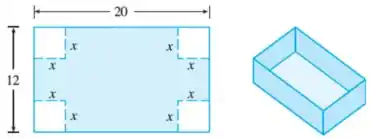
c) Uma caixa sem tampa deve ser construída de um pedaço retangular de papelão com dimensões por . Para isso, devem-se cortar quadrados de lados de cada canto e depois dobrar, conforme mostra a figura. Expresse o volume da caixa como uma função de .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão queremos desenvolver uma função que descreva o volume de uma caixa sem tampa que é construída a partir de um papelão por em função da sua altura
Tem alguma ideia do que fazer? 😉
Primeiro vamos obter uma função que será a função volume da caixa sendo sua altura.
Depois disso, vamos obter o domínio dessa função, ou seja, os possíveis valores que pode assumir em .
Sacou? Bora começar! 😁
Passo 2
A fórmula que descreve o volume de uma caixa, é dada por
Onde é a área da base e é a altura.
A área da base é dada pelo produto entre os lados da base, ou seja
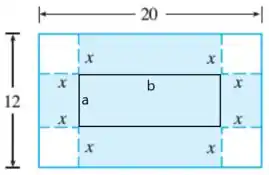
Pela figura, vemos que o lado é dado por e o lado é dado por .
Portanto a área da base é dada por
Legal, né? 😁
Passo 3
Substituindo no volume da caixa, temos
Como e passando para ...
E finalmente, obtendo o domínio dessa função, temos que analisar se existe alguma restrição para valores de .
Como é um polinômio, não temos restrição para , então pode assumir qualquer valor positivo.
É isso! Essa resolução te ajudou? Responde Aí! ✌
