UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 1, Questão 4d
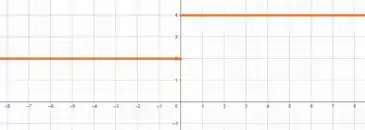
4. Encontre o domínio e esboce o gráfico da função.
d)
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema, queremos obter o domínio e o esboço do gráfico da função .
Parece tranquilo? 🤔
Para obter o domínio de uma função, podemos fazer uma analogia com uma receita de uma pizza...
Em uma receita, adicionamos os ingredientes na massa e levamos ao forno.
O domínio de uma função é todos os valores possíveis que a função pode adquirir na variável, ou seja, os possíveis valores para . Assim como os ingredientes da pizza pode ser considerado como o domínio da pizza.
Já para obter o gráfico de uma função, podemos obter alguns pontos dela e estimar o comportamento da função entre os pontos.
Sacou? Bora começar! 😁
Passo 2
Primeiro vamos obter o domínio de , pra isso, vamos analisar a função.
Na função vemos que há restrições para , já que em uma fração, não é possível fazer uma divisão por .
Portanto, o denominador de tem que ser diferente de
Logo, o domínio de é todos os valores reais menos o número .
Legal, né? 😎
Passo 3
Agora vamos esboçar o gráfico de .
Como temos um modulo no numerador, a função se comporta como para e para .
O que fizemos foi substituir por quando e por quando .
Assim, quando , a função é constante e igual a e quando a função é constante e igual a , ou seja
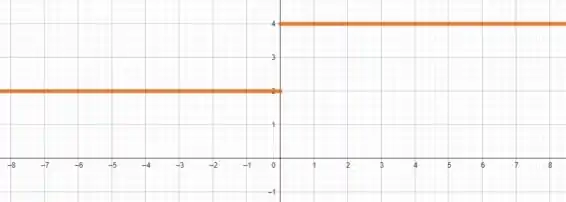
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
