USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.1g
1.1. Para cada função dada, determine o domínio e faça um esboço dele:
g)
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema queremos obter o domínio da função e obter um esboço do seu gráfico.
Parece tranquilo? 👀
Para obter o domínio de uma função, temos que analisar a função em si e se perguntar quais os possíveis valores as variáveis podem admitir para que a função seja definida no espaço real.
Legal, né? 😊
Já para obter o gráfico da função, podemos usar algumas arte manhas, como por exemplo obter algumas curvas de níveis da função fazendo e definindo algum valor para onde seja definido, ou também fixar alguma das variáveis a um constante e esboçar seu gráfico em duas dimensões no plano onde a variável foi fixada.
Entendeu? Bora lá! 😉
Passo 2
Vamos começar analisando a função .
Vemos que a função se trata de uma função logarítmica e com base nas características da função sabemos que esta só é definida se , ou seja, se o conteúdo dentro do for maior que .
Trazendo isso para o nosso problema, temos que
Com isso, nosso domínio da função pode ser descrito como
Bacana, não é? 😁
Passo 3
Por fim, para esboçar o gráfico de vamos usar o método dos níveis fazendo
Elevando os dois lados por , temos
Com isso vemos que os níveis de serão elipses dadas por
Ou seja, quanto maior o nível , menor é a elipse já quanto maior , mais o nível de tende a
Assim, podemos obter o gráfico de como
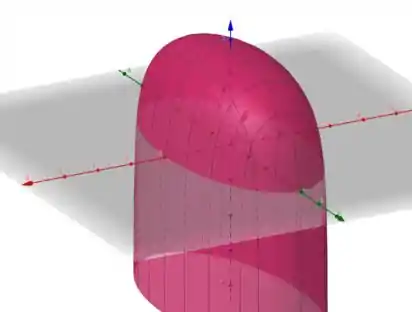
Sacou como faz? Responde Aí! 😉