Em cada caso identifique e represente graficamente o domínio da função .
Passo 1
Oiie, tudo bem?
O enunciado nos dá duas funções, sendo elas
e, precisamos determinar o domínio destas funções! Isso significa, analisar as funções para obter limitações nos valores de , o caminho costuma sempre ser analisar expressões algébricas que surgem devido a restrições dadas pelo formato da função! Vamos começar com a primeira alternativa! Vem comigo!
Passo 2
Temos que determinar o domínio da função
Aqui nós temos duas limitações! Lembre que nos reais, não existem raízes de números negativos! Portanto, precisamos que
e
Portanto, os limites são dados por
e
Uma parábola e uma reta! O domínio é então dado por
Isso pode ser representado no plano! Vamos fazer isso rapidinho! A representação no plano é tal que
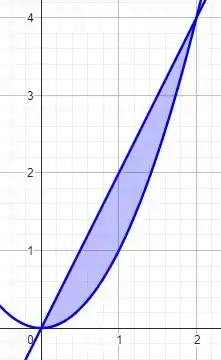
Vamos para a próxima agora! O processo é o mesmo!
Passo 3
Temos a função
Novamente, não queremos valores negativos dentro da raiz! Portanto
ou, simplesmente
Ou seja, temos um domínio tal que
Vamos representar no plano! Temos que
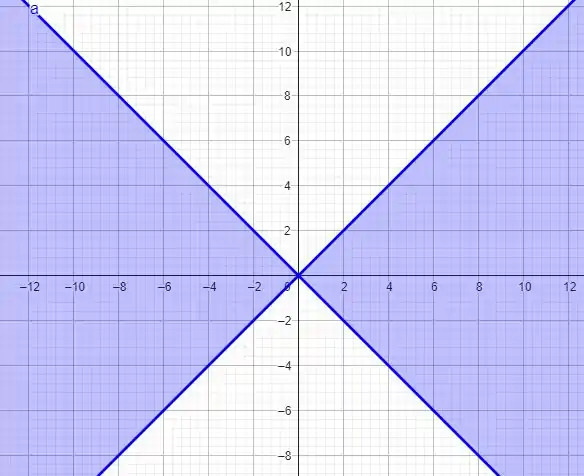
A questão é isso! Te vejo na próxima! Tchauzinho!